一个箱中原来装有大小相同的 5 个球,其中 3 个红球,2 个白球.规定:进行一次操 作是指“从箱中随机取出一个球,如果取出的是红球,则把它放回箱中;如果取出的是白 球,则该球不放回,并另补一个红球放到箱中.”
(1)求进行第二次操作后,箱中红球个数为 4 的概率;
(2)求进行第二次操作后,箱中红球个数的分布列和数学期望.
解:(1)设A
1表示事件“第一次操作从箱中取出的是红球”,
B
1表示事件“第一次操作从箱中取出的是白球”,
A
2表示事件“第二次操作从箱中取出的是红球”,
B
2表示事件“第二次操作从箱中取出的是白球”.
则A
1B
2表示事件“第一次操作从箱中取出的是红球,第二次操作从箱中取出的是白球”.
由条件概率计算公式得P(A
1B
2)=P(A
1)P(B
2|A
1)=
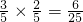
.
B
1A
2表示事件“第一次操作从箱中取出的是白球,第二次操作从箱中取出的是红球”.
由条件概率计算公式得P(B
1A
2)=P(B
1)P(A
2|B
1)=
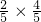
=
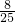
.
A
1B
2+B
1A
2表示“进行第二次操作后,箱中红球个数为 4”,又A
1B
2与B
1A
2是互斥事件.
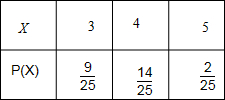
∴P(A
1B
2+B
1A
2)=P(A
1B
2)+P(B
1A
2)=
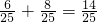
.
(2)设进行第二次操作后,箱中红球个数为X,则X=3,4,5.
P(X=3)
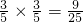
,P(X=4)=
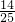
,
P(X=5)=
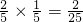
.
进行第二次操作后,箱中红球个数X的分布列为:
进行第二次操作后,箱中红球个数X的数学期望
EX=

=
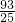
.
分析:(1)“进行第二次操作后,箱中红球个数为 4”,包括事件“第一次操作从箱中取出的是红球,第二次操作从箱中取出的是白球”和事件“第一次操作从箱中取出的是白球,第二次操作从箱中取出的是红球”,利用条件概率和互斥事件的概率计算公式即可得出.
(2)设进行第二次操作后,箱中红球个数为X,则X=3,4,5.利用相互独立事件的概率计算公式即可得出概率和分布列,再利用数学期望计算公式即可得出.
点评:熟练掌握分类讨论思想方法、条件概率和互斥事件的概率计算公式、相互独立事件的概率计算公式、数学期望计算公式是解题的关键.

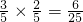 .
.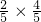 =
=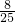 .
.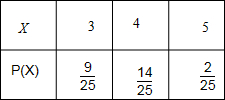
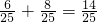 .
.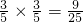 ,P(X=4)=
,P(X=4)=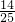 ,
,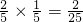 .
. =
=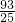 .
.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案