本题考查点轨迹方程的求法,两点间的距离公式的应用,体现了分类讨论的数学思想,注意考虑切线的斜率不存在的情况,这是易错点
(1)设P(x,y),由|AB|=2,且P为AB的中点,可得|OP|=1,由两点间的距离公式求得点P的轨迹方程.
(2)①当切线的斜率不存在时,由条件易得x=1符合条件;②当切线的斜率存在时,设出切线方程,由切线的性质可解得斜率k的值,用点斜式求得切线方程.
解: (1) 方法一:设P(x , y ),
∵∣AB∣=2,且P为AB的中点,
∴∣OP∣=1 ……………………2分
∴点P的轨迹方程为x
2+y
2=1. ……………………4分
方法二:设P(x , y ), ∵P为AB的中点,
∴A (2x , 0 ), B(0 , 2y ), ………………………2分
又∵∣AB∣=2 ∴(2x)
2+(2y)
2=2
化简得点P的轨迹C的方程为x
2+y
2=1. ……………4分
(2) ①当切线的斜率不存在时,切线方程为x=1,
由条件易得 x=1符合条件; ………………5分
②当切线的斜率存在时,设切线方程为 y-2=k(x-1) 即kx-y+2-k=0
由
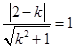
得k=
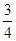
, ∴切线方程为y-2=
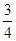
(x-1)
即 3x-4y+5=0
综上,过点M(1,2)且和轨迹C相切的直线方程为:
x=1 或3x-4y+5=0 ……………………8分

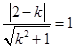 得k=
得k=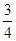 , ∴切线方程为y-2=
, ∴切线方程为y-2=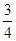 (x-1)
(x-1)

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案