
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
(I)估计这次测试数学成绩的平均分;
(II)假设在[90,100]段的学生的数学成绩都不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数中任意抽取2个数,有放回地抽取了3次,记这3次抽取中,恰好是两个学生的数学成绩的次数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.
(I)72分;(II)详见解析.
解析试题分析:(I)利用每组的数据的中值估算抽样学生的平均分,类似于加权平均数的算法,让每一段的中值乘以这一段对应的频率,得到平均数,利用样本的平均数来估计总体的平均数;
(II)根据等可能事件的概率公式得到两个数恰好是两个学生的数学成绩的概率,随机变量ξ的可能取值为0、1、2、3,且变量符合二项分布,根据符合二项分布写出分布列和期望,也可以用一般求期望的方法来解.
试题解析:(I)利用中值估算抽样学生的平均分:
45×0.05+55×0.15+65×0.2+75×0.3+85×0.25+95×0.05=72. (3分)
众数的估计值为75分 (5分)
所以,估计这次考试的平均分是72分. (6分)
(注:这里的众数、平均值为估计量,若遗漏估计或大约等词语扣一分)
(II)从95, 96,97,98,99,100中抽2个数的全部可能的基本结果数是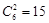 ,
,
有15种结果,学生的成绩在[90,100]段的人数是0.005×10×80=4(人),
这两个数恰好是两个学生的数学成绩的基本结果数是 ,
,
两个数恰好是两个学生的数学成绩的概率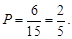 (8分)
(8分)
随机变量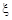 的可能取值为0、1、2、3,则有.
的可能取值为0、1、2、3,则有.
∴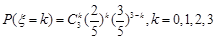
∴变量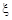 的分布列为:
的分布列为:
(10分)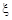
0 1 2 3 P 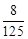
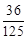
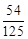
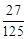

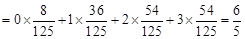 (12分)
(12分)
解法二. 随机变量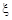 满足独立重复试验,所以为二项分布,即
满足独立重复试验,所以为二项分布,即 (10分)
(10分) (12分).
(12分).
考点: 1.离散型随机变量的期望与方差;2.频率分布直方图;3.离散型随机变量及其分布列.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:解答题
某地粮食需求量逐年上升,下表是部分统计数据:
| 年份(年) | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量 (万吨) | 236 | 246 | 257 | 276 | 286 |
 =
= x+
x+ .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2013年某市某区高考文科数学成绩抽样统计如下表:
(1)求出表中m、n、M、N的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;(纵坐标保留了小数点后四位小数)
(2)若2013年北京市高考文科考生共有20000人,试估计全市文科数学成绩在90分及90分以上的人数;
(3)香港某大学对内地进行自主招生,在参加面试的学生中,有7名学生数学成绩在140分以上,其中男生有4名,要从7名学生中录取2名学生,求其中恰有1名女生被录取的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
城市公交车的数量若太多则容易造成资源的浪费;若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:分钟):
| 组别 | 候车时间 | 人数 |
| 一 |  | 2 |
| 二 |  | 6 |
| 三 |  | 4 |
| 四 |  | 2 |
| 五 |  | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
城市公交车的数量太多容易造成资源的浪费,太少又难以满足乘客需求,为此,某市公交公司在某站台的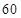 名候车乘客中随机抽取
名候车乘客中随机抽取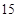 人,将他们的候车时间作为样本分成
人,将他们的候车时间作为样本分成 组,如下表所示(单位:min):
组,如下表所示(单位:min):
| 组别 | 候车时间 | 人数 |
| 一 |  |  |
| 二 |  | 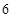 |
| 三 |  |  |
| 四 |  |  |
| 五 |  |  |
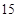 名乘客的平均候车时间;
名乘客的平均候车时间;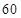 名乘客中候车时间少于
名乘客中候车时间少于 分钟的人数;
分钟的人数;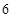 人中选
人中选 人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照 ,
, ,
, ,
, ,
, 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在 ,
, 的数据).
的数据).
频率分布直方图 茎叶图
(Ⅰ)求样本容量n和频率分布直方图中x、y的值;
(Ⅱ)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到市政广场参加环保知识宣传的志愿者活动,求所抽取的2名同学来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对甲、乙两种商品重量的误差进行抽查,测得数据如下(单位:mg):
甲:13 15 14 14 9 14 21 9 10 11
乙:10 14 9 12 15 14 11 19 22 16
(1)画出样本数据的茎叶图,并指出甲、乙两种商品重量误差的中位数;
(2)计算甲种商品重量误差的样本方差;
(3)现从重量误差不低于15的乙种商品中随机抽取2件,求重量误差为19的商品被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某次有1000人参加的数学摸底考试,其成绩的频率分布直方图如图所示,规定85分及其以上为优秀.
(1)下表是这次考试成绩的频数分布表,求正整数a, b的值;
| 区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
| 人数 | 50 | a | 350 | 300 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学高三年级从甲、乙两个班级各选出七名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,
(1)求x和y的值;
(2)计算甲班七名学生成绩的方差;
(3)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
参考公式:方差 其中
其中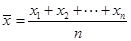
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com