
分析 由恒等式an=a1•$\frac{{a}_{2}}{{a}_{1}}$•$\frac{{a}_{3}}{{a}_{2}}$•…•$\frac{{a}_{n}}{{a}_{n-1}}$,结合等比数列的通项公式,化简可得数列{an}的通项,即可得到所求值.
解答 解:由题意可得an=a1•$\frac{{a}_{2}}{{a}_{1}}$•$\frac{{a}_{3}}{{a}_{2}}$•…•$\frac{{a}_{n}}{{a}_{n-1}}$
=1•2•22•…•2n-1=21+2++n-1=${2}^{\frac{1}{2}n(n-1)}$,
即有数列{an}的第100顶等于${2}^{\frac{1}{2}×100×99}$=24950.
故答案为:24950.
点评 本题考查数列的通项的求法,注意运用数列的恒等式,同时考查等比数列的通项公式的运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤2} | B. | {x|-1≤x<2} | C. | {x|-1<x<2} | D. | {x|-2<x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值是$\frac{5}{4}$,最小值是1 | B. | 最大值是1,最小值是$\frac{1}{4}$-$\sqrt{3}$ | ||
| C. | 最大值是2,最小值是$\frac{1}{4}$-$\sqrt{3}$ | D. | 最大值是2,最小值是$\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 92 | 85 | 95 |
| 面试 | 85 | 95 | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
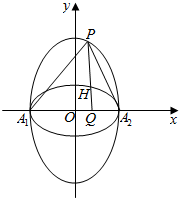 若两个椭圆的离心率相等,则称它们为“相似椭圆”.如图,在直角坐标系xOy中,已知椭圆C1:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,A1,A2分别为椭圆C1的左右顶点,椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”
若两个椭圆的离心率相等,则称它们为“相似椭圆”.如图,在直角坐标系xOy中,已知椭圆C1:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,A1,A2分别为椭圆C1的左右顶点,椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com