Question

某工艺品加工厂准备生产具有收藏价值的奥运会标志--“中国印•舞动的北京”和奥运会吉祥物--“福娃”．该厂所用的主要原料为A、B两种贵金属，已知生产一套奥运会标志需用原料A和原料B的量分别为4盒和3盒，生产一套奥运会吉祥物需用原料A和原料B的量分别为5盒和10盒．若奥运会标志每套可获利700元，奥运会吉祥物每套可获利1200元，该厂月初一次性购进原料A、B的量分别为200盒和300盒．问该厂生产奥运会标志和奥运会吉祥物各多少套才能使该厂月利润最大？最大利润为多少？

Answer 1

分析：本题考查的知识点是简单线性规划的应用，由已知我们可设该厂每月生产奥运会标志和奥运会吉祥物分别为x，y套，月利润为z元，则根据已知中生产一套奥运会标志需用原料A和原料B的量分别为4盒和3盒，生产一套奥运会吉祥物需用原料A和原料B的量分别为5盒和10盒．若奥运会标志每套可获利700元，奥运会吉祥物每套可获利1200元，该厂月初一次性购进原料A、B的量分别为200盒和300盒．我们可以列出变量x，y的约束条件及目标函数Z的解析式，利用线性规划的方法，易求出答案．

解答：解：设该厂每月生产奥运会标志和奥运会吉祥物分别为x，y套，月利润为z元，
由题意得

4x+5y≤200 3x+10y≤300 x≥0 y≥0

目标函数为z=700x+1200y．
作出二元一次不等式组所表示的平面区域，即可行域，如图：


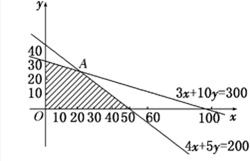
目标函数可变形为y=-

7

12

x+

z

1200

，
∵-

4

5

＜-

7

12

＜-

3

10

，
∴当y=

-7

12

x+

z

1200

通过图中的点A时，

z

1200

最大，z最大．解

4x+5y=200 32+10y=300

得点A坐标为（20，24）．
将点A（20，24）代入z=700x+1200y
得z_max=700×20+1200×24=42800元．
答：该厂生产奥运会标志和奥运会吉祥物分别为20、24套时月利润最大，最大利润为42800元．

点评：在解决线性规划的应用题时，其步骤为：①分析题目中相关量的关系，列出不等式组，即约束条件?②由约束条件画出可行域?③分析目标函数Z与直线截距之间的关系?④使用平移直线法求出最优解?⑤还原到现实问题中．