
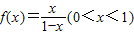 的反函数为f-1(x),数列{an}和{bn}满足:
的反函数为f-1(x),数列{an}和{bn}满足: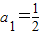 ,an+1=f-1(an),函数y=f-1(x)的图象在点(n,f-1(n))(n∈N*)处的切线在y轴上的截距为bn.
,an+1=f-1(an),函数y=f-1(x)的图象在点(n,f-1(n))(n∈N*)处的切线在y轴上的截距为bn.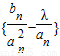 ;的项中仅
;的项中仅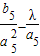 最小,求λ的取值范围;
最小,求λ的取值范围;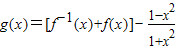 ,0<x<1.数列{xn}满足:
,0<x<1.数列{xn}满足: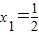 ,0<xn<1且xn+1=g(xn),(其中n∈N*).证明:
,0<xn<1且xn+1=g(xn),(其中n∈N*).证明: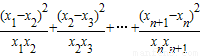
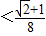 .
.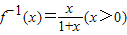 .
.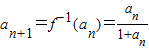 ,由此能求出数列{an}的通项公式;
,由此能求出数列{an}的通项公式;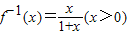 ,知
,知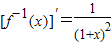 ,所以y=f-1(x)在点(n,f-1(n))处的切线方程为
,所以y=f-1(x)在点(n,f-1(n))处的切线方程为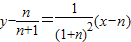 ,由此入手能求出λ的取值范围.
,由此入手能求出λ的取值范围.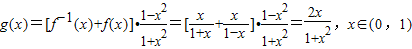 .所以
.所以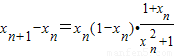 ,又因0<xn<1,则xn+1>xn.由此入手能够证明
,又因0<xn<1,则xn+1>xn.由此入手能够证明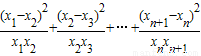
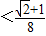 .
. ,解得
,解得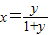 ;由0<x<1,解得y>0.
;由0<x<1,解得y>0.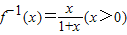 .
.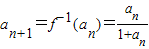 ,
,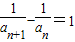 .
.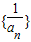 是以2为首项,1为公差的等差数列,故
是以2为首项,1为公差的等差数列,故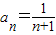 .(4分)
.(4分)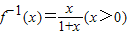 ,∴
,∴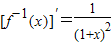 ,
,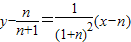 ,
,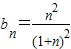 .∴
.∴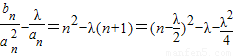 .
.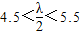 .
.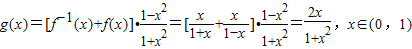 .
.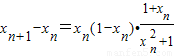 ,
,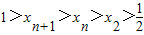 .
.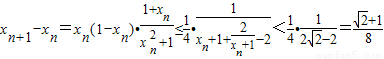
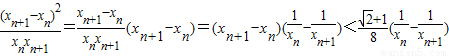
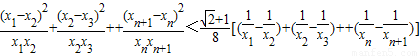
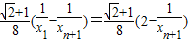 (12分)
(12分)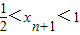 ,∴
,∴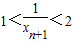 ,∴
,∴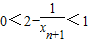
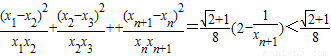 (14分)
(14分)

科目:高中数学 来源:2009-2010学年四川省攀枝花市高三(上)第二次月考数学试卷(理科)(解析版) 题型:解答题
 的反函数为f-1(x),数列{an}满足:a1=1,an+1=f-1(an)(n∈N*).
的反函数为f-1(x),数列{an}满足:a1=1,an+1=f-1(an)(n∈N*).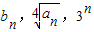 成等比数列,数列{bn}的前n项和为Sn,求Sn.
成等比数列,数列{bn}的前n项和为Sn,求Sn.查看答案和解析>>
科目:高中数学 来源:高考数学最后冲刺必读题解析30讲(22)(解析版) 题型:解答题
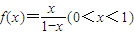 的反函数为f-1(x),数列{an}和{bn}满足:
的反函数为f-1(x),数列{an}和{bn}满足: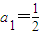 ,an+1=f-1(an),函数y=f-1(x)的图象在点(n,f-1(n))(n∈N*)处的切线在y轴上的截距为bn.
,an+1=f-1(an),函数y=f-1(x)的图象在点(n,f-1(n))(n∈N*)处的切线在y轴上的截距为bn.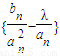 ;的项中仅
;的项中仅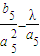 最小,求λ的取值范围;
最小,求λ的取值范围;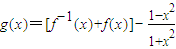 ,0<x<1.数列{xn}满足:
,0<x<1.数列{xn}满足: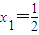 ,0<xn<1且xn+1=g(xn),(其中n∈N*).证明:
,0<xn<1且xn+1=g(xn),(其中n∈N*).证明: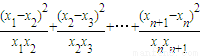
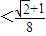 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com