

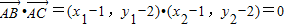
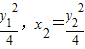 代入①式化简得-2(y1+y2)-y1y2=20③10′
代入①式化简得-2(y1+y2)-y1y2=20③10′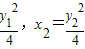 代入②式化简得BC的方程为(y1+y2)y-y1y2=4x④12′
代入②式化简得BC的方程为(y1+y2)y-y1y2=4x④12′

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2009-2010学年广东省广州市越秀区高三摸底数学试卷(理科)(解析版) 题型:解答题
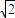 ,0),并且与定圆C:
,0),并且与定圆C: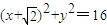 (圆心为C)相切.
(圆心为C)相切.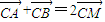 ?如果存在,求出k的值;如果不存在,请说明理由.
?如果存在,求出k的值;如果不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:2011年高三数学第一轮基础知识训练(25)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com