解:(1)依题意,G(x)=x+2.
设利润函数为p(x),
则p(x)=
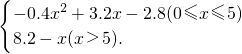
(4分)
(2)要使工厂有赢利,
即解不等式p(x)>0,(5分)
当0≤x≤5时,
解不等式-0.4x
2+3.2x-2.8>0,
即x
2-8x+7<0,
∴1<x<7.
∴1<x≤5; (7分)
当x>5时,解不等式8.2-x>0,
得x<8.2,
∴5<x<8.2.(9分)
综上,要使工厂赢利,x应满足1<x<8.2,
即产品应控制在大于100台且小于820台的范围 (11分)
(3)0≤x≤5时,
f(x)=-0.4(x-4)
2+3.6.
故当x=4时,f(x)有最大值3.6. (14分)
而当x>5时,
f(x)<8.2-5=3.2.
所以,当工厂生产400台产品时,赢利最多.(16分)
分析:(1)依题意,G(x)=x+2.设利润函数为p(x),由题设条件写出利润函数p(x)的函数表达式.
(2)要使工厂有赢利,即解不等式p(x)>0,当0≤x≤5时,解不等式-0.4x
2+3.2x-2.8>0,得1<x≤5;当x>5时,解不等式8.2-x>0,得5<x<8.2.由此知要使工厂赢利,产品应控制在大于100台且小于820台的范围.
(3)0≤x≤5时,f(x)=-0.4(x-4)
2+3.6.故当x=4时,f(x)有最大值3.6.而当x>5时,f(x)<8.2-5=3.2.由此可知当工厂生产400台产品时,赢利最多.
点评:本题考查函数在生产实际中的具体运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

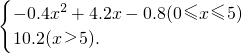
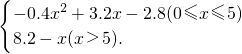 (4分)
(4分)

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案