
某农场预算用5600元购买单价为50元(每吨)的钾肥和20元(每吨)的氮肥,希望使两种肥料的总数量(吨)尽可能的多,但氮肥吨数不少于钾肥吨数,且不多于钾肥吨数的1.5倍.
(1) 设买钾肥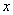 吨,买氮肥
吨,买氮肥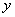 吨,按题意列出约束条件、画出可行域,并求钾肥、氮肥各买多少才行?
吨,按题意列出约束条件、画出可行域,并求钾肥、氮肥各买多少才行?
(2) 设点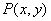 在(1)中的可行域内,求
在(1)中的可行域内,求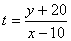 的取值范围;
的取值范围;
(3) 已知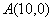 ,O是原点,
,O是原点, 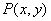 在(1)中的可行域内,求
在(1)中的可行域内,求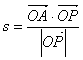 的取值范围.
的取值范围.
解:(1)设肥料总数为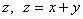 ,
……1分
,
……1分
由题意得约束条件
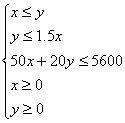 ,即
,即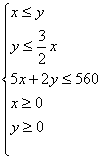 , ……3分
, ……3分
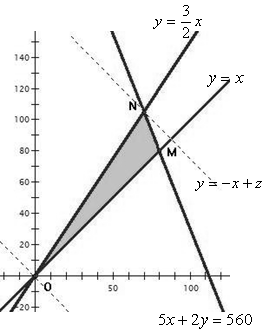
画出可行域(如图) ……4分
目标函数: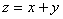 ,即
,即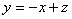 ,表示斜率为
,表示斜率为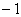 ,
,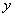 轴上截距为
轴上截距为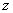 的平行直线系.
的平行直线系.
当直线过点N时,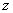 最大.
最大.
联立方程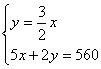 ,解得
,解得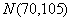 ……5分
……5分
此时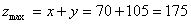 .
……6分
.
……6分
 购买钾肥70吨,氮肥105吨时,两种肥料的总数量最大为175吨.……
购买钾肥70吨,氮肥105吨时,两种肥料的总数量最大为175吨.……
(2)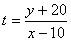 表示(1)中可行域内动点
表示(1)中可行域内动点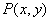 与定点
与定点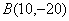 连线的斜率. ……7分
连线的斜率. ……7分
联立方程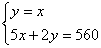 ,解得
,解得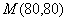
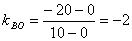 ,
, ,
……9分
,
……9分
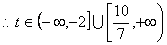 ……10分
……10分
(3)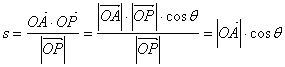 ,
,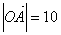 ,
,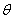 为
为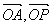 的夹角
的夹角
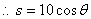 .
有图可知:
……11分
.
有图可知:
……11分
当点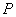 在线段
在线段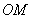 时,
时,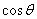 最大为
最大为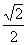 ,此时s最大值为
,此时s最大值为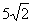 ; ……12分
; ……12分
当点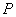 在线段
在线段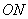 时,
时,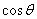 最小为
最小为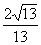 ,此时s最小值为
,此时s最小值为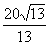 .
……13分
.
……13分
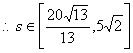 ……14分
……14分
另解: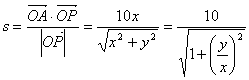 ,
,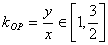 ,代入可得
,代入可得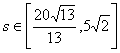


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com