Question

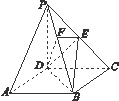
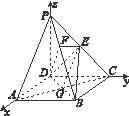
如图，在四棱锥P－ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD＝DC=2，E是PC的中点，作EF⊥BP交BP于点F．

(1)证明：PA∥平面EDB；

(2)证明：PB⊥平面EFD．

 

Answer 1

证明：以D为坐标原点，射线DA，DC，DP分别为x，y，z轴的正方向建立空间直角坐标系．设DC＝2

(1)  连接AC，AC交BD于G，连接EG.依题意得A(2,0,0)，P(0,0，2)，E（0,1,1）.

因为底面ABCD是正方形，所以G是此正方形的中心，故点G的坐标为（1,1，0），

且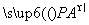＝(2,0，－2)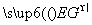，＝（1,0，-1）.所以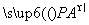＝2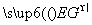，这表明PA∥EG.而EG⊂平面EDB且PA⊄平面EDB，所以PA∥平面EDB.

(2)依题意得B(2，2，0)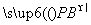，＝(2，2，－2)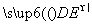．＝（0,1,1），故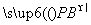·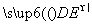＝0＋2-2＝0，所以PB⊥DE，由已知EF⊥PB，且EF∩DE＝E，所以PB⊥平面EFD.