一般地,我们把函数h(x)=anxn+an-1xn-1+…+a1x+a(n∈N)称为多项式函数,其中系数a,a1,…,an∈R.
设 f(x),g(x)为两个多项式函数,且对所有的实数x等式f[g(x)]=g[f(x)]恒成立.
(Ⅰ) 若f(x)=x2+3,g(x)=kx+b(k≠0).
①求g(x)的表达式;
②解不等式f(x)-g(x)>5.
(Ⅱ)若方程f(x)=g(x)无实数解,证明方程f[f(x)]=g[g(x)]也无实数解.
【答案】
分析:(Ⅰ)根据已知条件f[g(x)]=g[f(x)]直接代入求解即可.
(Ⅱ)证明无解考虑用反证法证明,假设有解,与已知条件推出矛盾.
解答:解:(Ⅰ)①∵f[g(x)]=g[f(x)]即(kx+b)
2+3=k(x
2+3)+b k
2x
2+2kbx+b
2+3=kx
2+3k+b
∴
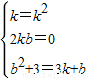
解得
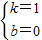
∴g(x)=x
②f(x)-g(x)>5,即x
2-x+3>5 解得 x>2或x<-1
(Ⅱ)反证法:F(x)=f(x)-g(x)则 F[f(x)]=f[f(x)]-g[f(x)]F[g(x)]=f[g(x)]-g[g(x)]若结论成立,则推出 F[f(x)]+F[g(x)]=0; 即F[f(x)]=-F[g(x)]说明存在一点a,a介于f(x)与g(x)之间,满足F(a)=0 因为f(x)=g(x)无实数解,则F(x)=0永远不成立,推出假设不成立,
方程f(x)=g(x)无实数解,方程f[f(x)]=g[g(x)]也无实数解.证毕
点评:把函数与方程的思想联系起来,以及用反证法证明无解是解决此题的关键.

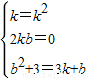 解得
解得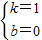 ∴g(x)=x
∴g(x)=x
