
已知二次函数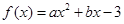 在
在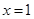 处取得极值,且在
处取得极值,且在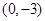 点处的切线与直线
点处的切线与直线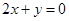 平行.
平行.
(1)求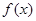 的解析式; (2)求函数
的解析式; (2)求函数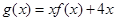 的单调递增区间及极值;
的单调递增区间及极值;
(3)求函数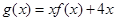 在
在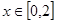 的最值.
的最值.
解: (1) 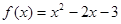 .
.
(2) 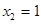 有极小值为0. 在
有极小值为0. 在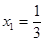 有极大值
有极大值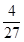 .
.
(3)由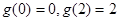 及(2),得,函数
及(2),得,函数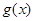 的最大值为2,最小值为0.
的最大值为2,最小值为0.
【解析】本题考查导数在求闭区间上函数最值的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答
(1)由f(x)=ax2+bx-3,知f′(x)=2ax+b.由二次函数f(x)=ax2+bx-3在x=1处取得极值,且在(0,-3)点处的切线与直线2x+y=0平行,知 f′(1)=2a+b=0,f′(0)=b=-2
,由此能求出f(x).(2)由f(x)=x2-2x-3,知g(x)=xf(x)+4x=x3-2x2+x,所以g′(x)=3x2-4x+1=(3x-1)(x-1).令g′(x)=0,得x1=
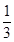 ,x2=1.列表讨论能求出函数g(x)=xf(x)+4x的单调递增区间及极值.
,x2=1.列表讨论能求出函数g(x)=xf(x)+4x的单调递增区间及极值.
(3)由g(0)=0,g(2)=2,结合(2)的结论,能求出函数g(x)的最大值和最小值.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
已知二次函数![]() 在
在![]() 处取得最小值
处取得最小值![]() .
.
(1)求![]() 的表达式;
的表达式;
(2)若任意实数![]() 都满足等式
都满足等式![]() (
(![]() 为多项式,
为多项式,![]() ),试用
),试用![]() 表示
表示![]() 和
和![]() ;
;
(3)设圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 与
与![]() 外切
外切![]() ,
,![]() 为各项都是正数的等比数列,记
为各项都是正数的等比数列,记![]() 为前
为前![]() 个圆的面积之和,
个圆的面积之和,![]() .
.
查看答案和解析>>
科目:高中数学 来源:2013届山西省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知二次函数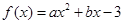 在
在 处取得极值,且在
处取得极值,且在 点处的切线与直线
点处的切线与直线 平行。
平行。
(1)求 的解析式;
的解析式;
(2)求函数 的单调递增区间及极值;
的单调递增区间及极值;
(3)求函数 在
在 的最值。
的最值。
查看答案和解析>>
科目:高中数学 来源:2010年福建省高二下学期期末考试理科数学卷 题型:解答题
(本小题满分14分) :
已知二次函数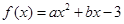 在
在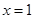 处取得极值,且在
处取得极值,且在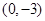 点处的切线与直线
点处的切线与直线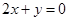 平行.
平行.
(1)求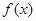 的解析式;
的解析式;
(2)求函数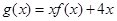 的单调递增区间与极值.
的单调递增区间与极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com