
 的最小值为0,其中
的最小值为0,其中
 的值;
的值; 有
有 ≤
≤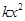 成立,求实数
成立,求实数 的最小值;
的最小值;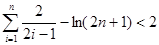 (
( ).
).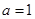 (2)
(2) 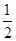 (3) 见解析
(3) 见解析 的定义域为
的定义域为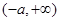
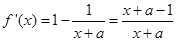
 ,得
,得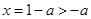
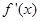 ,
, 的变化情况如下表:
的变化情况如下表:| x | 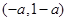 | 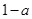 | 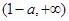 |
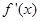 | - | 0 | + |
 | 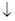 | 极小值 | 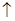 |
 在
在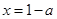 处取得最小值,故由题意
处取得最小值,故由题意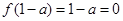 ,所以
,所以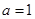
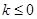 时,取
时,取 ,有
,有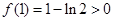 ,故
,故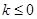 时不合题意.当
时不合题意.当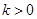 时,令
时,令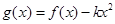 ,即
,即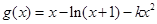
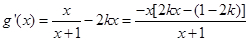
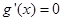 ,得
,得
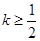 时,
时,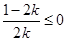 ,
,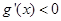 在
在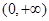 上恒成立。因此
上恒成立。因此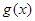 在
在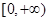 上单调递减.从而对于任意的
上单调递减.从而对于任意的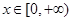 ,总有
,总有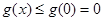 ,即
,即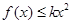 在
在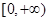 上恒成立,故
上恒成立,故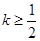 符合题意.
符合题意.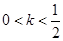 时,
时,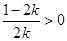 ,对于
,对于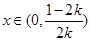 ,
, ,故
,故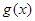 在
在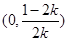 上单调递增.因此当取
上单调递增.因此当取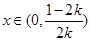 时,
时,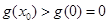 ,即
,即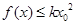 不成立.
不成立.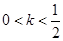 不合题意.
不合题意.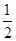 .
.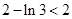 =右边,所以不等式成立.
=右边,所以不等式成立.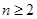 时,
时,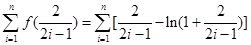
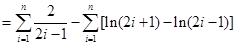
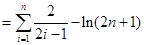
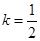 ,得
,得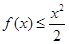
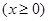 ,
,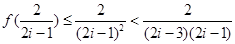
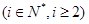
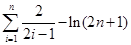
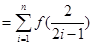
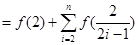
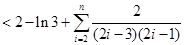
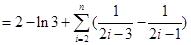
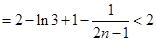
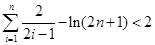 ,
,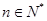


科目:高中数学 来源:不详 题型:单选题
 是定义在
是定义在 上的函数,其图象是一条连续的曲线,且满足下列条件:①
上的函数,其图象是一条连续的曲线,且满足下列条件:① 的值域为M,且MÍ
的值域为M,且MÍ ;②对任意不相等的
;②对任意不相等的 ,
, ∈
∈ , 都有|
, 都有| -
- |<|
|<| -
- |.那么,关于
|.那么,关于 的方程
的方程 =
= 在区间
在区间 上根的情况是 ( )
上根的情况是 ( )| A.没有实数根 | B.有且仅有一个实数根 |
| C.恰有两个不等的实数根 | D.有无数个不同的实数根 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 立方米时,只付基本费9元和每户每月定额损耗费
立方米时,只付基本费9元和每户每月定额损耗费 元;
元; 立方米时,除了付基本费9元和定额损耗费外,超过部分每立方米付
立方米时,除了付基本费9元和定额损耗费外,超过部分每立方米付 元的超额费;
元的超额费; 不超过5元。
不超过5元。 (元)与月用水量
(元)与月用水量 (立方米)的函数关系式;
(立方米)的函数关系式;| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 4 | 17 |
| 二 | 5 | 23 |
| 三 | 2.5 | 11 |
 的值。
的值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为
,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为 米与
米与 米均不小于2米,且要求“转角处”(图中矩形
米均不小于2米,且要求“转角处”(图中矩形 )的面积为8平方米
)的面积为8平方米 表示草坪的面积
表示草坪的面积 ,并指出
,并指出 的取值范围
的取值范围 、
、 ,才能使草坪的面积最大?并求出草坪的最大面积。
,才能使草坪的面积最大?并求出草坪的最大面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com