
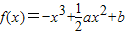 .
. ,求y=f(x)的解析式并确定其单调区间;
,求y=f(x)的解析式并确定其单调区间;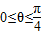 时a的取值范围.
时a的取值范围. ,所以在在x=1处的导数等于0,且在x=1处的函数值为
,所以在在x=1处的导数等于0,且在x=1处的函数值为 ,就可得到两个关于a,b的等式,解出a,b求出函数的解析式.再列表判断函数在那个范围内导数大于0,即为增区间,在那个范围内导数小于0,即为减区间.
,就可得到两个关于a,b的等式,解出a,b求出函数的解析式.再列表判断函数在那个范围内导数大于0,即为增区间,在那个范围内导数小于0,即为减区间.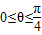 时,0≤k≤1,而切线的斜率又是函数在切点处的导数,所以当x∈(0,1]时,f(x)的图象上任意一点处的导数属于[0,1],这样就可得到含参数a的不等式0≤-3x2+ax≤1在x∈(0,1]上恒成立,再据此求出参数a的范围.
时,0≤k≤1,而切线的斜率又是函数在切点处的导数,所以当x∈(0,1]时,f(x)的图象上任意一点处的导数属于[0,1],这样就可得到含参数a的不等式0≤-3x2+ax≤1在x∈(0,1]上恒成立,再据此求出参数a的范围.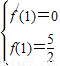
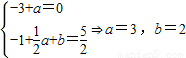 ,
,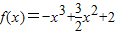
| x | (-∞,0) | (0,1) | 1 | (1,+∞) | |
| f′(x) | - | + | - | ||
| f(x) | 递减 | 递增 | 递减 |
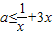 ,
,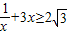 (当且仅当
(当且仅当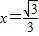 时取等号),∴
时取等号),∴ ,
,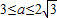


科目:高中数学 来源:2012-2013学年浙江省宁波市海曙区效实中学高一(上)期末数学试卷(3-11班)(解析版) 题型:解答题
 ,
,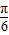 个单位后,再将得到的函数图象上的各点横坐标伸长到原来的2倍,得到函数g(x),若
个单位后,再将得到的函数图象上的各点横坐标伸长到原来的2倍,得到函数g(x),若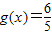 ,求
,求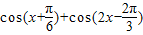 的值.
的值.查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市东城区示范校高三(下)3月联考数学试卷(文科)(解析版) 题型:解答题
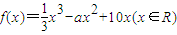 .
.查看答案和解析>>
科目:高中数学 来源:2010年北京市宣武区高考数学一模试卷(理科)(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:2010年北京市一模试卷及高频考点透析:导数与定积分(解析版) 题型:解答题
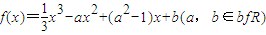 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com