
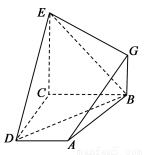
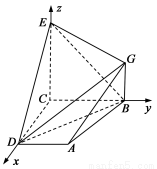
如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且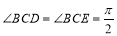 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
(1)求证:AG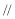 平面BDE;
平面BDE;
(2)求:二面角G DE
DE B的余弦值.
B的余弦值.
(1)见解析(2)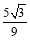
【解析】
试题分析:(1)由题设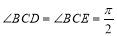 ,平面ABCD⊥平面BCEG,可证
,平面ABCD⊥平面BCEG,可证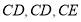 两两垂直,据此建设立以
两两垂直,据此建设立以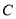 为坐标原点的空间直角坐标系,写出
为坐标原点的空间直角坐标系,写出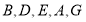 诸点的坐标,求出平面
诸点的坐标,求出平面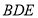 的一个法向量
的一个法向量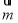 ,由于
,由于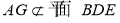 ,要证AG
,要证AG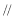 平面BDE,只要证
平面BDE,只要证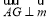 即可;
即可;
(2)设平面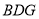 的一个法向量为
的一个法向量为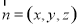 ,由
,由 求出的坐标,最后利用向量
求出的坐标,最后利用向量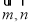 求出二面角G
求出二面角G DE
DE B的余弦值.
B的余弦值.
试题解析:
【解析】
由平面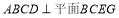 ,平面
,平面
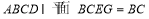 ,
,
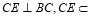 平面BCEG,
平面BCEG, 
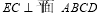 ,
,
由平面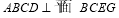 ,
,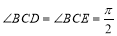 知
知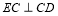 ,.2分
,.2分
根据题意建立如图所示的空间直角坐标系,可得
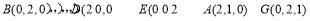 .3分
.3分
(1)设平面BDE的法向量为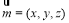 ,则
,则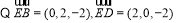
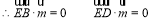
 即
即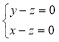 ,
, 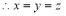 ,
,
 平面BDE的一个法向量为
平面BDE的一个法向量为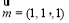 ..5分
..5分
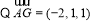
 ,
,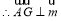 ,
,
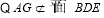 ,∴AG∥平面BDE. .7分
,∴AG∥平面BDE. .7分
(2)由(1)知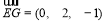
设平面EDG的法向量为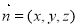 ,则
,则 即
即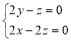
 平面EDG的一个法向量为
平面EDG的一个法向量为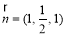 ..9分
..9分
又平面BDE的一个法向量为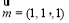 ,
,
设二面角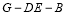 的大小为
的大小为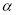 ,则
,则 ,
,
 二面角
二面角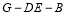 的余弦值为
的余弦值为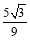 .12分
.12分
考点:1、空间直角坐系;2、利用空间向量的数量积判断空间中直线与平面的位置关系;3、利用空间向量的夹角求二面角的平面角的余弦.


科目:高中数学 来源:2013-2014学年山东省高三12月月考理科数学试卷(解析版) 题型:选择题
将函数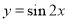 的图象向右平移
的图象向右平移 个单位,再向上平移1个单位,所得函数图象对应的解析式为 ( )
个单位,再向上平移1个单位,所得函数图象对应的解析式为 ( )
A.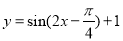 B.
B.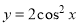
C.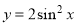 D.
D.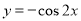
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省高三12月月考文科数学试卷(解析版) 题型:选择题
在△ABC中,内角A、B、C的对边分别是a、b、c,若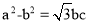 ,
, ,则A=( )
,则A=( )
A.30° B.60°
C.120° D.150°
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省菏泽市高三3月模拟考试理科数学试卷(解析版) 题型:填空题
设关于x,y的不等式组 表示的平面区域内存在点P(x0,y0)满足x0-2y0=2,则m的取值范围是 .
表示的平面区域内存在点P(x0,y0)满足x0-2y0=2,则m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省菏泽市高三3月模拟考试理科数学试卷(解析版) 题型:选择题
某程序框图如图所示,现将输出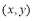 值依次记为:
值依次记为: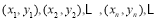 若程序运行中输出的一个数组是
若程序运行中输出的一个数组是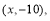 则数组中的
则数组中的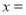 ( )
( )

A.32 B.24 C.18 D.16
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省菏泽市高三3月模拟考试文科数学试卷(解析版) 题型:选择题
已知函数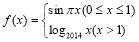 ,若a、b、c互不相等,且
,若a、b、c互不相等,且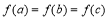 ,则a+b+c的取值范围是( )
,则a+b+c的取值范围是( )
A.(1,2014) B.(1,2015) C.(2,2015) D.[2,2015]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com