
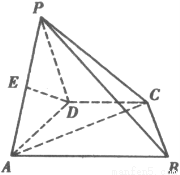
如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD与底面ABCD垂直,E为PA的中点.
(1)求证: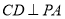
(2)求证:DE∥平面PBC;
(1)证明见解析;(2)证明见解析
【解析】
试题分析:(1)证明线线垂直时,要注意题中隐含的垂直关系,如等腰三角形的底边上的高,中线和顶角的角平分线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形等等;(2)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;四是利用线面平行的定义,一般用反证法;(3)利用判断定理证明有关问题时,要把条件写全,不用漏掉一些条件,注意转化思想的应用
试题解析:证明:(1)∵AD⊥AB,CD∥AB,
∴ 2分
2分
又∵侧面 与底面ABCD垂直且交线为
与底面ABCD垂直且交线为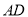 ,
,
∴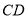 垂直侧面
垂直侧面 4分
4分
又∵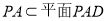 ∴
∴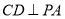 6分
6分
(2)如图,取AB的中点F,连接DF,EF.
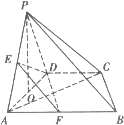
在直角梯形ABCD中,CD∥AB,且AB=4,CD=2,所以 ,
,
所以四边形BCDF为平行四边形,所以DF∥BC 8分
又∵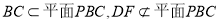
∴DF∥平面PBC.
在△PAB中,PE=EA,AF=FB,所以EF//PB. 9分
又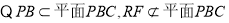
∴ ∥平面
∥平面
又因为 ,
,
所以平面 ∥平面
∥平面 . 11分
. 11分
因为
 平面
平面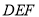 ,所以
,所以 ∥平面
∥平面 . 12分
. 12分
考点:(1)证明直线与直线垂直;(2)证明直线与平面平行.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源:2016届福建省高一下学期第二次阶段考数学试卷(解析版) 题型:选择题
下列说法正确的是( )
A.三点确定一个平面
B.不重合的两个平面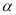 和
和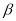 可以有不在同一条直线上的三个公共点
可以有不在同一条直线上的三个公共点
C.四边形一定是平面图形
D.梯形一定是平面图形
查看答案和解析>>
科目:高中数学 来源:2016届福建省高一下学期第一阶段考试数学试卷(解析版) 题型:选择题
平面 与平面
与平面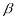 平行的条件可以是( )
平行的条件可以是( )
A. 内有无穷多条直线与
内有无穷多条直线与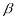 平行 B.直线a//
平行 B.直线a// ,a//
,a//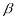
C.直线a ,直线b
,直线b ,且a//
,且a//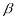 ,b//
,b// D.
D. 内的任何直线都与
内的任何直线都与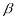 平行
平行
查看答案和解析>>
科目:高中数学 来源:2016届福建省晋江市高一年下学期期中考试数学试卷(解析版) 题型:选择题
给定函数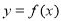 的图像如下列图中,经过原点和(1,1),且对任意
的图像如下列图中,经过原点和(1,1),且对任意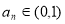 ,由关系式
,由关系式 得到数列{
得到数列{ },满足
},满足 ,则该函数的图像为( )
,则该函数的图像为( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com