
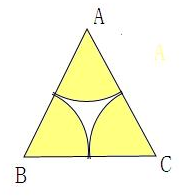
 解:满足条件的正三角形ABC如下图所示:
解:满足条件的正三角形ABC如下图所示:
| ||
| 4 |
| 3 |
| 1 |
| 2 |
| S空白部分 |
| S三角形 |
| ||||
|
| π | ||
2
|
| N(A) |
| N |


科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
 一个水平放置的△ABC用斜二测画法画出的直观图是如图2-7-3所示的边长为1的正△A'B'C',则在真实图形中AB边上的高是
一个水平放置的△ABC用斜二测画法画出的直观图是如图2-7-3所示的边长为1的正△A'B'C',则在真实图形中AB边上的高是| 6 |
| 6 |
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 4 |
查看答案和解析>>
科目:高中数学 来源:四川省双流中学2011-2012学年高二上学期期中考试数学文科试题 题型:022
在底面边长为2的正四棱锥(底面是正方形,且顶点在底面的射影是底面中心的四棱锥)P-ABCD中,若侧棱PA与底面ABCD所成的角为![]() ,则此正四棱锥的顶点P到边AB的距离为________.
,则此正四棱锥的顶点P到边AB的距离为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省苏州市张家港外国语学校高二(上)周日数学试卷10(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com