
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,N为
,N为![]() 的中点.
的中点.
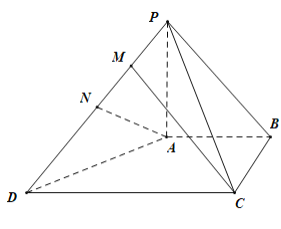
(1)求证:![]() 平面
平面![]()
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值
(3)在线段![]() 上是否存在一点M,使得直线
上是否存在一点M,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由
的值;若不存在,说明理由
【答案】(1)见解析;(2)![]() (3)存在,
(3)存在,![]()
【解析】
(1)首先过![]() 作
作![]() ,垂足为
,垂足为![]() ,以
,以![]() 为坐标原点,分別以
为坐标原点,分別以![]() ,
,![]() ,
,![]() 为
为![]() 轴建立空间直角坐标系,分别求出
轴建立空间直角坐标系,分别求出![]() 和平面
和平面![]() 的法向量
的法向量![]() ,根据
,根据![]() 即可证明
即可证明![]() 平面
平面![]() .
.
(2)求出平面![]() 的法向量为
的法向量为![]() ,再代入二面角公式计算即可得到答案.
,再代入二面角公式计算即可得到答案.
(3)首先假设线段![]() 上存在一点
上存在一点![]() ,设
,设![]() ,
,![]() ,得到
,得到![]() ,根据直线
,根据直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求得
,求得![]() ,所以存在
,所以存在![]() ,且
,且![]() .
.
(1)过![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() ,
,
以![]() 为坐标原点,分別以
为坐标原点,分別以![]() ,
,![]() ,
,![]() 为
为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
如图所示:
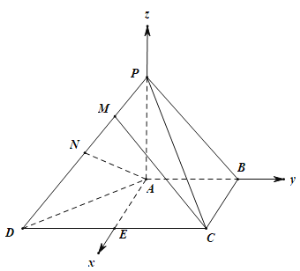
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]()
![]() ,
,![]() ,
,
则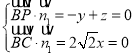 ,令
,令![]() ,解得:
,解得:![]() .
.
因为![]() ,所以
,所以![]()
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
因为![]() ,
,![]() ,
,
所以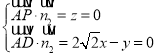 ,令
,令![]() ,解得
,解得![]() .
.
所以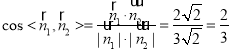 .
.
即平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值![]() .
.
(3)假设线段![]() 上存在一点
上存在一点![]() ,设
,设![]() ,
,![]() ,
,![]() .
.
因为![]() ,所以
,所以![]()
则![]()
因为平面![]() 的一个法向量
的一个法向量![]()
所以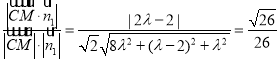 ,
,
整理得:![]() ,
,
所以![]() ,因为
,因为![]() ,所以
,所以![]() .
.
所以存在![]() ,且
,且![]() .
.


科目:高中数学 来源: 题型:
【题目】已知在![]() 上任意一点
上任意一点![]() 处的切线
处的切线![]() 为
为![]() ,若过右焦点
,若过右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,已知在点
两点,已知在点![]() 处切线相交于
处切线相交于![]() .
.
(Ⅰ)求![]() 点的轨迹方程;
点的轨迹方程;
(Ⅱ)①若过点![]() 且与直线
且与直线![]() 垂直的直线(斜率存在且不为零)交椭圆
垂直的直线(斜率存在且不为零)交椭圆![]() 于
于![]() 两点,证明
两点,证明![]() 为定值.
为定值.
②四边形![]() 的面积是否有最小值,若有请求出最小值;若没有请说明理由.
的面积是否有最小值,若有请求出最小值;若没有请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() 3,g(x)=alnx﹣2x(a∈R).
3,g(x)=alnx﹣2x(a∈R).
(1)讨论g(x)的单调性;
(2)是否存在实数a,使不等式f(x)≥g(x)恒成立?如果存在,求出a的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年寒假是特殊的寒假,因为疫情全体学生只能在家进行网上在线学习,为研究学生网上学习的情况,某校社团对男女各10名学生进行了网上在线学习的问卷调查,每名学生给出评分(满分100分),得到如图所示的茎叶图.
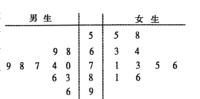
(1)根据茎叶图判断男生组和女生组哪个组对网课的评价更高?并说明理由;
(2)如图是按该20名学生的评分绘制的频率分布直方图,求![]() 的值并估计这20名学生评分的平均值(同一组中的数据用该组区间中点值作为代表);
的值并估计这20名学生评分的平均值(同一组中的数据用该组区间中点值作为代表);
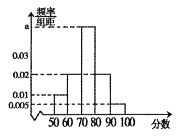
(3)求该20名学生评分的中位数![]() ,并将评分超过
,并将评分超过![]() 和不超过
和不超过![]() 的学生数填入下面的列联表:
的学生数填入下面的列联表:
超过 | 不超过 | |
男生 | ||
女生 |
根据列联表,能否有![]() 的把握认为男生和女生的评分有差异?
的把握认为男生和女生的评分有差异?
附: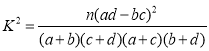 ,
,
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地为鼓励群众参与“全民读书活动”,增加参与读书的趣味性.主办方设计这样一个小游戏:参与者抛掷一枚质地均匀的骰子(正方体,六个面上分别标注1,2,3,4,5,6六个数字).若朝上的点数为偶数.则继续抛掷一次.若朝上的点数为奇数,则停止游戏,照这样的规则进行,最多允许抛掷3次.每位参与者只能参加一次游戏.
(1)求游戏结束时朝上点数之和为5的概率;
(2)参与者可以选择两种方案:方案一:游戏结束时,若朝上的点数之和为偶数,奖励3本不同的畅销书;若朝上的点数之和为奇数,奖励1本畅销书.方案二:游戏结束时,最后一次朝上的点数为偶数,奖励5本不同的畅销书,否则,无奖励.试分析哪一种方案能使游戏参与者获得更多畅销书奖励?并说明判断的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大约在20世纪30年代,世界上许多国家都流传着这样一个题目:任取一个正整数![]() ,如果它是偶数,则除以2;如果它是奇数,则将它乘以3加1,这样反复运算,最后结果必然是1.这个题目在东方被称为“角谷猜想”,世界一流的大数学家都被其卷入其中,用尽了各种方法,甚至动用了最先进的电子计算机,验算到对700亿以内的自然数上述结论均为正确的,但却给不出一般性的证明.例如取
,如果它是偶数,则除以2;如果它是奇数,则将它乘以3加1,这样反复运算,最后结果必然是1.这个题目在东方被称为“角谷猜想”,世界一流的大数学家都被其卷入其中,用尽了各种方法,甚至动用了最先进的电子计算机,验算到对700亿以内的自然数上述结论均为正确的,但却给不出一般性的证明.例如取![]() ,则要想算出结果1,共需要经过的运算步数是( )
,则要想算出结果1,共需要经过的运算步数是( )
A.9B.10C.11D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,![]() .
.
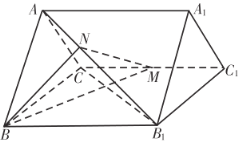
(1)求证:![]() 平面
平面![]() ;
;
(2)条件①:直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ;
;
条件②:![]() 为锐角,三棱锥
为锐角,三棱锥![]() 的体积为
的体积为![]() .
.
在以上两个条件中任选一个,补充在下面的问题中,并解决该问题:
若平面![]() 平面
平面![]() ,______,求平面
,______,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com