
分析 可根据条件先画出图形,然后找出过P,M,N的平面:根据MN∥A1C1∥AC,从而找过P平行于AC的直线,这样就可找出过点M,N,P的平面,并求出该直线和DC的交点,从而结合图形即可求出PQ的长度.
解答 解:如图,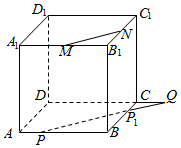
在BC上取$C{P}_{1}=\frac{a}{3}$,连接PP1;
则MN∥PP1,延长PP1,则交DC延长线于Q;
∴PQ=PP1+P1Q=$\frac{2\sqrt{2}}{3}a+\frac{\sqrt{2}}{3}a=\sqrt{2}a$.
故答案为:$\sqrt{2}a$.
点评 考查正方体的画法,数形结合解题的方法,以及平行线分线段成比例定理,两平行线可确定一平面,直角三角形的边的关系,三角函数定义.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
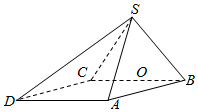 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知:∠ABC=45°,AB=2,BC=2$\sqrt{2}$,SB=SC,直线SD与平面ABCD所成角的正弦值为$\frac{\sqrt{11}}{11}$.O为BC的中点.
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知:∠ABC=45°,AB=2,BC=2$\sqrt{2}$,SB=SC,直线SD与平面ABCD所成角的正弦值为$\frac{\sqrt{11}}{11}$.O为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,3] | B. | [2,$\frac{23}{8}$] | C. | [$\frac{5}{16}$,$\frac{9}{16}$] | D. | [$\frac{27}{16}$,$\frac{9}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{6}$或$\frac{7π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com