
 (x>0)上,且与直线3x+4y+3=0相切的面积最小的圆的方程为 .
(x>0)上,且与直线3x+4y+3=0相切的面积最小的圆的方程为 . 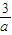 ),a>0,圆心到直线的最短距离为:
),a>0,圆心到直线的最短距离为: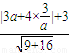 ,再由a的值化简,并利用均值不等式求出r的最小值,即可求出圆的方程.
,再由a的值化简,并利用均值不等式求出r的最小值,即可求出圆的方程.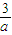 ),a>0,
),a>0,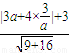 =
=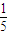 |3a+
|3a+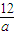 +3|=r
+3|=r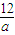 +3|=5r
+3|=5r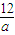 +3=5r
+3=5r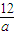 +3≥2
+3≥2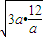 +3=15
+3=15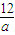 ,即a=2时,取等号,
,即a=2时,取等号, )
) )2=9
)2=9

科目:高中数学 来源:广州模拟 题型:单选题
| 2 |
| x |
| A.(x-1)2+(y-2)2=5 | B.(x-2)2+(y-1)2=5 |
| C.(x-1)2+(y-2)2=25 | D.(x-2)2+(y-1)2=25 |
查看答案和解析>>
科目:高中数学 来源:泉州模拟 题型:单选题
| 3 |
| x |
A.(x-2)2+(y-
| B.(x-3)2+(y-1)2=(
| ||||||
C.(x-1)2+(y-3)2=(
| D.(x-
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com