
已知数列 的首项
的首项 .
.
(1)求证: 是等比数列,并求出
是等比数列,并求出 的通项公式;
的通项公式;
(2)证明:对任意的 ;
;
(3)证明: .
.
(1) ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
解析试题分析:(1)将 两边去倒数并常量分量,然后所得式子变形数列{
两边去倒数并常量分量,然后所得式子变形数列{ }的第n+1项是第n项若干倍形式,根据等比数列定义即可判定{
}的第n+1项是第n项若干倍形式,根据等比数列定义即可判定{ }是等比数列,利用等比数列通项公式,先求出{
}是等比数列,利用等比数列通项公式,先求出{ }的通项公式,再解出
}的通项公式,再解出 的通项公式;(2)将不等式右侧式子配凑
的通项公式;(2)将不等式右侧式子配凑 的通项公式形式,再将其化为关于
的通项公式形式,再将其化为关于 的二次函数最值问题,通过放缩即可证明该不等式;(3)先将
的二次函数最值问题,通过放缩即可证明该不等式;(3)先将 的通项公式常量分量,代入
的通项公式常量分量,代入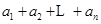 ,通过放缩即可证明不等式的左半部分,对
,通过放缩即可证明不等式的左半部分,对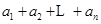 利用(2)的结论缩小,出现首项为
利用(2)的结论缩小,出现首项为 ,公比为
,公比为 的等比数列的前n项和,数列取
的等比数列的前n项和,数列取 为该数列前n项和的算术平局值,即可证明该不等式右半部分.
为该数列前n项和的算术平局值,即可证明该不等式右半部分.
试题解析:(1) ,又
,又
所以 是以
是以 为首项,以
为首项,以 为公比的等比数列.
为公比的等比数列. 5分
5分
(2)由(1)知

 9分
9分
(3)先证左边不等式,由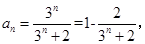 知
知 ;当
;当 时等号成立; 11分
时等号成立; 11分
再证右边不等式,由(2)知,对任意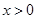 ,有
,有 ,
,
取 ,
,
则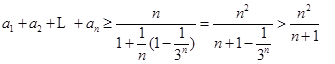 14分
14分
考点:等比数列定义、通项公式、前n项和公式;二次函数最值;放缩法;转化与化归思想;运算求解能力


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:解答题
将数列 中的所有项按每一行比上一行多两项的规则排成如下数表:
中的所有项按每一行比上一行多两项的规则排成如下数表:
已知表中的第一列数 构成一个等差数列, 记为
构成一个等差数列, 记为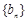 , 且
, 且 , 表中每一行正中间一个数
, 表中每一行正中间一个数 构成数列
构成数列 , 其前n项和为
, 其前n项和为 .
.
(1)求数列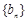 的通项公式;(2)若上表中, 从第二行起, 每一行中的数按从左到右的顺序均构成等比数列, 公比为同一个正数, 且
的通项公式;(2)若上表中, 从第二行起, 每一行中的数按从左到右的顺序均构成等比数列, 公比为同一个正数, 且 .①求
.①求 ;②记
;②记 , 若集合M的元素个数为3, 求实数
, 若集合M的元素个数为3, 求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列 中,
中, ,
, .
.
(1)求 ,
, 的值;
的值;
(2)求证: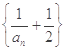 是等比数列,并求
是等比数列,并求 的通项公式
的通项公式 ;
;
(3)数列 满足
满足 ,数列
,数列 的前n项和为
的前n项和为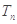 ,若不等式
,若不等式 对一切
对一切 恒成立,求
恒成立,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com