
已知函数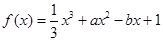 (
(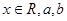 为实数)有极值,且在
为实数)有极值,且在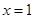 处的切线与直线
处的切线与直线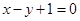 平行.
平行.
(1)求实数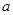 的取值范围;
的取值范围;
(2)是否存在实数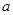 ,使得函数
,使得函数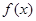 的极小值为
的极小值为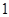 ,若存在,求出实数
,若存在,求出实数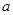 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)设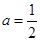 ,
,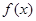 的导数为
的导数为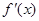 ,令
,令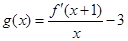
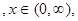
求证: 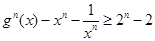
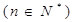
(1) 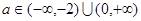 (2)存在
(2)存在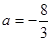 . (3)略
. (3)略
【解析】
(1)根据极值的信息,则选用导数法,先求f'(x),再由f(x)有极值,可有=a2-4b>0,又由在x=-1处的切线与直线x-y+1=0平行,可得f'(-1)=1-a+b=1从而求解
(2)先假存在,则根据条件,则有关于a的不等式,进而得到范围。
(3)构造函数利用导数的思想求解函数的最值得到证明
(1)∵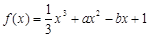 ,∴
,∴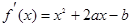 ,
,
由题意∴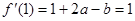 ,
,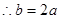 ①
……2分
①
……2分
∵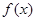 有极值,∴方程
有极值,∴方程 有两个不等实根.
有两个不等实根.
∴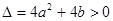 、 ∴
、 ∴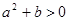 . ②
. ②
由①、②可得,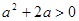 . ∴
. ∴ 或
或 .
.
故实数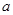 的取值范围是
的取值范围是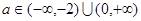 …2分
…2分
(2)存在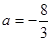 .……………1分
.……………1分
由(1)令 ,
,
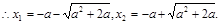

∴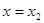 时,
时,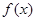 取极小值,则
取极小值,则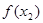 =
=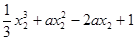
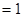 ,
,
∴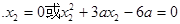 ……………………………………………………2分
……………………………………………………2分
若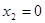 ,即
,即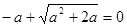 则
则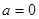 (舍).……………………1分
(舍).……………………1分
若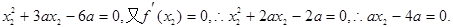
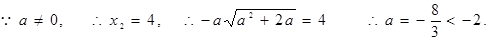
∴存在实数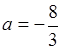 ,使得函数
,使得函数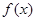 的极小值为1 ………1分
的极小值为1 ………1分
(3)∵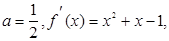
 ,
,
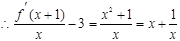
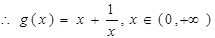 …….l分
…….l分

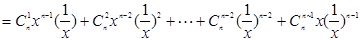
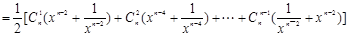
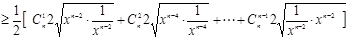
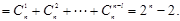
∴其中等号成立的条件为 ………………3分
………………3分


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
已知函数![]() ,
,![]() 为实数)有极值,且在
为实数)有极值,且在![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(1)求实数a的取值范围;
(2)是否存在实数a,使得函数![]() 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
(3)设![]()
求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011年辽宁省高二下学期期中考试理科数学 题型:解答题
(本小题满分12分)
已知函数 ,
, 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线 平行.
平行.
(I)求实数a的取值范围;
(II)是否存在实数a,使得函数 的极小值为1,若存在,求出实数a的值;若不存
的极小值为1,若存在,求出实数a的值;若不存
在,请说明理由;
(Ⅲ)设
求证: .
.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年广州市七区联考高二数学(理)下学期期末监测 题型:解答题
(本小题满分14分)
已知函数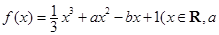 ,
,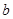 为实数)有极值,且在
为实数)有极值,且在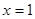 处的切线与直线
处的切线与直线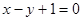 平行.
平行.
(1)求实数a的取值范围;
(2)设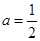 ,
,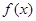 的导数为
的导数为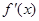 ,令
,令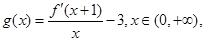
求证: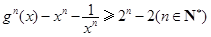 .
.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年广州市七区联考高二数学(文)下学期期末监测 题型:解答题
(本小题满分14分)
已知函数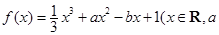 ,
,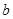 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线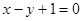 平行.
平行.
(1)求实数a的取值范围;
(2)是否存在实数a,使得函数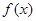 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分) 已知函数![]() ,
,![]() 为实数)有极值,且在
为实数)有极值,且在![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(I)求实数a的取值范围;
(II)是否存在实数a,使得函数![]() 的极小值为1,若存在,求出实数a的值;若不存
的极小值为1,若存在,求出实数a的值;若不存
在,请说明理由;
(Ⅲ)设![]()
求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com