
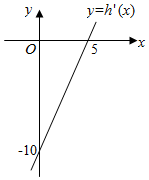 已知二次函数h(x)=ax2+bx+c(c<4),其导函数y=h'(x)的图象如图所示,函数f(x)=8lnx+h(x).
已知二次函数h(x)=ax2+bx+c(c<4),其导函数y=h'(x)的图象如图所示,函数f(x)=8lnx+h(x).分析 (1)利用导函数y=h′(x)的图象确定a,b的值即可;
(2)要使求函数f(x)在区间(m,m+$\frac{1}{2}$)上是单调增函数,则f'(x)的符号没有变化,可以求得实数m的取值范围;
(3)函数y=kx的图象总在函数y=f(x)图象的上方得到kx大于等于f(x),列出不等式,构造函数,求出函数的最小值即可得到c的范围.
解答 解:(1)二次函数h(x)=ax2+bx+c的导数为:
y=h′(x)=2ax+b,由导函数y=h′(x)的图象可知,
导函数y=h′(x)过点(5,0)和(0,-10),
代入h′(x)=2ax+b得:
b=-10,a=1;
(2)由(1)得:h(x)=x2-10x+c,h′(x)=2x-10,
f(x)=8lnx+h(x)=8lnx+x2-10x+c,
f′(x)=$\frac{8}{x}$+2x-10=$\frac{2(x-1)(x-4)}{x}$,
当x变化时
| (0,1) | 1 | (1,4) | 4 | (4,+∞) | |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | ↘ | ↗ |
点评 本题考查学生会利用导数求曲线上过某点切线方程的斜率,会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值.综合性较强,难度较强.


科目:高中数学 来源: 题型:解答题
 某中学选取20名优秀同学参加2016年数学应用知识竞赛,将他们的成绩(百分制,均为整数)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],共6组后,得到频率分布直方图(如图),根据图中的信息,回答下列问题.
某中学选取20名优秀同学参加2016年数学应用知识竞赛,将他们的成绩(百分制,均为整数)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],共6组后,得到频率分布直方图(如图),根据图中的信息,回答下列问题.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1,2} | B. | {0,1,2} | C. | {0,1} | D. | {1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
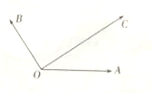 如图所示,平面内有三个向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角为90°,且|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=2,|$\overrightarrow{OC}$|=2$\sqrt{3}$,若$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,(λ,μ∈R)则( )
如图所示,平面内有三个向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角为90°,且|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=2,|$\overrightarrow{OC}$|=2$\sqrt{3}$,若$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,(λ,μ∈R)则( )| A. | λ=4,μ=2 | B. | λ=4,μ=1 | C. | λ=2,μ=1 | D. | λ=2,μ=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com