
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 举例a=i,即可判断①错;运用共轭复数的概念,计算即可判断②对;由复数乘法的运算性质,可得③对;由两数的乘积性质可得④对;当a=i,b=1,可得⑤错;当a=1,b=1+i,c=1-i,即可判断⑥错;
运用不等式的性质:两边同时加上一个实数或整式,不等式符号不改变,即可判断⑦对.
解答 解:对于非零复数a,b,c,
①当a=i,则a+$\frac{1}{a}$=i+$\frac{1}{i}$=i-i=0,故①错;
②若a=-$\overline{a}$,$\overline{a}$为a的共轭复数,且a为非零复数,
设a=x+yi(x,y∈R),即有x+yi=-(x-yi),可得x=0,y≠0,则a为纯虚数,故②对;
③由复数乘法的运算性质可得(a+b)2=a2+2ab+b2,故③对;
④若a2=ab,即a(a-b)=0,由a为非零复数,则a=b,故④对;
⑤当a=i,b=1,则|a|=|b|=1,则a=±b不成立.故⑤错;
⑥当a=1,b=1+i,c=1-i,有a2+b2+c2=1+2i-2i=1>0,但a2+b2=1+2i,c2=-2i,
无法比较a2+b2,-c2,故⑥错;
⑦若a2+b2>-c2,可得不等式左右两边均为实数,由不等式的性质:两边同时加上一个实数或整式,
不等式符号不改变.则a2+b2+c2>0.故⑦对.
综上可得,真命题的个数为4.
故选:C.
点评 本题考查复数的概念、运算和性质,注意与实数比较,考查判断能力和推理能力,属于基础题和易错题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11}{5}$ | B. | $\frac{11}{5}$i | C. | -$\frac{11}{5}$ | D. | -$\frac{11}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3f(2)<2f(3) | B. | 3f(2)>2f(3) | C. | 2f(2)<3f(3) | D. | 2f(2)>3f(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
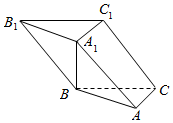 如图,在斜三棱柱ABC-A1B1C1中,A1B⊥AC,且A1B=AC=5,AA1=BC=13,且AB=12.
如图,在斜三棱柱ABC-A1B1C1中,A1B⊥AC,且A1B=AC=5,AA1=BC=13,且AB=12.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
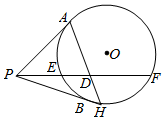 已知点P是圆O外的一点,过P作圆O的切线PA,PB,切点为A,B,过P作一割线交圆O于点E,F,若2PA=PF,取PF的中点D,连接AD,并延长交圆于H.
已知点P是圆O外的一点,过P作圆O的切线PA,PB,切点为A,B,过P作一割线交圆O于点E,F,若2PA=PF,取PF的中点D,连接AD,并延长交圆于H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com