
 已知三棱柱ABC-A1B1C1,侧面AA1C1C⊥侧面ABB1A1,AA1=A1C=CA=2,
已知三棱柱ABC-A1B1C1,侧面AA1C1C⊥侧面ABB1A1,AA1=A1C=CA=2,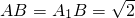 .
.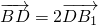 ,在线段CA1上是否存在一点E,使得DE∥平
,在线段CA1上是否存在一点E,使得DE∥平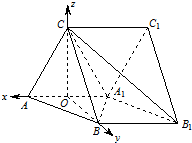 证明:(1)取AA1中点O,连接CO,BO.
证明:(1)取AA1中点O,连接CO,BO. 由对称性知,二面角A-BC-A1的大小为二面角A-BC-O的两倍
由对称性知,二面角A-BC-A1的大小为二面角A-BC-O的两倍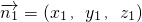 是平面ABC的一个法向量,
是平面ABC的一个法向量,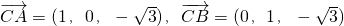 ,
,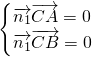 即
即 解得
解得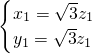
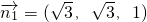 .
.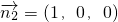 是平面OBC的一个法向量,
是平面OBC的一个法向量,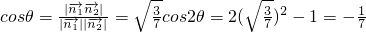 ,
, .
.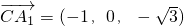 ,故可设
,故可设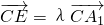 =
=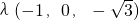 ,
,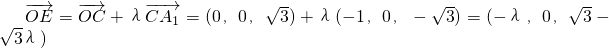 ,
,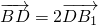 ,
,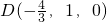 ,
,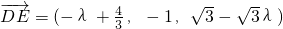 ,
,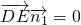 ,
,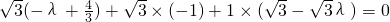 ,解得
,解得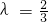 ,
,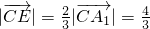
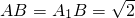 .易得CO⊥AA1且BO⊥AA1,结合线面垂直的判定定理可得AA1⊥平面BOC,进而由线面垂直的性质定理得到AA1⊥BC;
.易得CO⊥AA1且BO⊥AA1,结合线面垂直的判定定理可得AA1⊥平面BOC,进而由线面垂直的性质定理得到AA1⊥BC;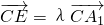 ,结合DE∥平面ABC,
,结合DE∥平面ABC,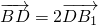 ,我们可以构造一个关于λ的方程,解方程求出λ的值,即可得到向量
,我们可以构造一个关于λ的方程,解方程求出λ的值,即可得到向量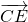 模的大小.
模的大小.

科目:高中数学 来源:2012-2013学年广东高二第二次月考文科数学试卷(解析版) 题型:填空题
已知三棱柱ABC-A´B´C´所有的棱长均为2,且侧棱与底面垂直,则该三棱柱的体积
是
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省云浮市高二(上)12月月考数学试卷(文科)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com