
科目:高中数学 来源:不详 题型:填空题
 中,如果存在非零的常数
中,如果存在非零的常数 ,使
,使 对于任意正整数
对于任意正整数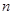 均成立,就称数列
均成立,就称数列 为周期数列,其中
为周期数列,其中 叫做数列
叫做数列 的周期. 已知数列
的周期. 已知数列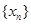 满足
满足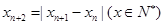 ,若
,若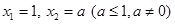 ,当数列
,当数列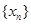 的周期为
的周期为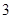 时,则数列
时,则数列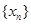 的前2012项的和为
的前2012项的和为 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.第1个出现的等式是:152 – 1 =" 224" |
| B.一般式是:(2n + 3)2 – 1 =" 4(n" + 1)(n+2) |
| C.当试验一直继续下去时,一定会出现等式1012 – 1 =10200 |
| D.24的倍数加1必是某一质数的完全平方 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中,
中, ,
, ,
, 的通项公式;
的通项公式; 的前
的前 项和
项和 ;
; 的最小项的值,并证明你的结论。
的最小项的值,并证明你的结论。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 :
: 、
、 、
、 且
且 (
( ),与数列
),与数列 :
: 、
、 、
、 、
、 且
且 (
( ).
). .
. ,求
,求 的值;
的值; 的值,并求证当
的值,并求证当 时,
时, ;
; ,且存在正整数
,且存在正整数 ,使得在
,使得在 ,
, ,
, ,
, 中有4项为100.求
中有4项为100.求 的值,并指出哪4项为100.
的值,并指出哪4项为100.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com