
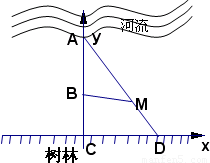
 树林的边界是直线l(如图所示),一只兔子在河边喝水时发现了一只狼,兔子和狼分别位于l的垂线AC上的点A点B点处,AB=BC=a(a为正常数),若兔子沿AD方向以速度2μ向树林逃跑,同时狼沿线段BM(M∈AD)方向以速度μ进行追击(μ为正常数),若狼到达M处的时间不多于兔子到达M处的时间,狼就会吃掉兔子.
树林的边界是直线l(如图所示),一只兔子在河边喝水时发现了一只狼,兔子和狼分别位于l的垂线AC上的点A点B点处,AB=BC=a(a为正常数),若兔子沿AD方向以速度2μ向树林逃跑,同时狼沿线段BM(M∈AD)方向以速度μ进行追击(μ为正常数),若狼到达M处的时间不多于兔子到达M处的时间,狼就会吃掉兔子.| BM |
| μ |
| AM |
| 2μ |
| 2a |
| 3 |
| 4a2 |
| 9 |
|2a-
| ||
|
| 2a |
| 3 |
| BM |
| μ |
| AM |
| 2μ |
| 2a |
| 3 |
| 4a2 |
| 9 |
| 2a |
| 3 |
| 2a |
| 3 |
| 4a2 |
| 9 |
|2a-
| ||
|
| 2a |
| 3 |
| 3 |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |


科目:高中数学 来源: 题型:解答题
 树林的边界是直线l(如图所示),一只兔子在河边喝水时发现了一只狼,兔子和狼分别位于l的垂线AC上的点A点B点处,AB=BC=a(a为正常数),若兔子沿AD方向以速度2μ向树林逃跑,同时狼沿线段BM(M∈AD)方向以速度μ进行追击(μ为正常数),若狼到达M处的时间不多于兔子到达M处的时间,狼就会吃掉兔子.
树林的边界是直线l(如图所示),一只兔子在河边喝水时发现了一只狼,兔子和狼分别位于l的垂线AC上的点A点B点处,AB=BC=a(a为正常数),若兔子沿AD方向以速度2μ向树林逃跑,同时狼沿线段BM(M∈AD)方向以速度μ进行追击(μ为正常数),若狼到达M处的时间不多于兔子到达M处的时间,狼就会吃掉兔子.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省无锡一中高二(上)期中数学试卷(成志班)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com