
 某单位准备印制一批书面材料,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲厂的印刷费用y(千元)与书面材料数量x(千份)的关系见下表:
某单位准备印制一批书面材料,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲厂的印刷费用y(千元)与书面材料数量x(千份)的关系见下表:| 书面材料数量x(千份) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 甲厂的印刷费用y(千元) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | … |
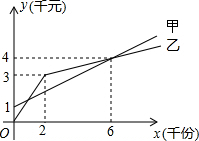 解:(1)由表格可知,甲厂的制版费为1千元,y甲=
解:(1)由表格可知,甲厂的制版费为1千元,y甲=| 1 |
| 2 |
|
|
| 1 |
| 4 |
| 5 |
| 2 |
|
|
|
|
| 1 |
| 2 |
| 1 |
| 4 |
| 5 |
| 2 |


科目:高中数学 来源: 题型:
| 8 |
| 15 |
| 3 |
| 4 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 8 |
| 15 |
| 3 |
| 4 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)某企业准备招聘一批大学生到本单位就业,但在签约前要对他们的某项专业技能进行测试.在待测试的某一个小组中有男、女生共10人(其中女生人数多于男生人数),如果从中随机选2人参加测试,其中恰为一男一女的概率为![]() ;
;
(Ⅰ)求该小组中女生的人数;
(Ⅱ)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为![]() ,每个男生通过的概率均为
,每个男生通过的概率均为![]() ;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量
;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三12周考理科数学 题型:解答题
(本小题满分12分)某企业准备招聘一批大学生到本单位就业,但在签约前要对他们的某项专业技能进行测试.在待测试的某一个小组中有男、女生共10人(其中女生人数多于男生人数),如果从中随机选2人参加测试,其中恰为一男一女的概率为 ;(Ⅰ)求该小组中女生的人数;(Ⅱ)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为
;(Ⅰ)求该小组中女生的人数;(Ⅱ)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为 ,每个男生通过的概率均为
,每个男生通过的概率均为 ;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量
;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com