
(1)求切线PA、PB所在直线的方程;
(2)求切线长|PA|;
(3)求∠APB的正弦值;
(4)求AB的方程.
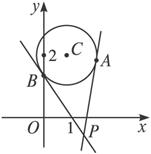
解:(1)如下图,设过P点的切线方程为l:y+1=k(x-2),即kx-y-2k-1=0.
∵l与圆C相切,
∴d=r,
即![]() .
.
∴k2-6k-7=0.
∴k=7或k=-1.
∴所求切线方程为y+1=7(x-2)或y+1=-(x-2),即7x-y-15=0或x+y-1=0.
(2)连结CA、PC,
在Rt△PAC中,|PC|=![]() ,|AC|=r=
,|AC|=r=![]() ,
,
∴|PA|=2![]() .
.
(3)在Rt△PCA中,设∠APC=θ,
∴sinθ=![]() ,cosθ=
,cosθ=![]() ,sin2θ=2sinθ·cosθ=2×
,sin2θ=2sinθ·cosθ=2×![]() ,即sin∠APB=
,即sin∠APB=![]() .
.
(4)易得以PC为直径的圆的方程为(x-![]() )2+(y-
)2+(y-![]() )2=
)2=![]() .
.
将其与已知圆(x-1)2+(y-2)2=2联立,相减可得出公共弦AB所在直线的方程:4x-12y+27=0.


科目:高中数学 来源: 题型:
A.30° B.30°或150° C.60° D.120°或60°
查看答案和解析>>
科目:高中数学 来源:2015届山西太原第五中学高二12月月考理科数学试卷(解析版) 题型:填空题
已知圆C:(x+1)2+y2=16及点A(1,0),Q为圆C上一点,AQ的垂直平分线交CQ于M则点M的轨迹方程为 .
查看答案和解析>>
科目:高中数学 来源:2015届山西太原第五中学高二12月月考文科数学试卷(解析版) 题型:填空题
已知圆C:(x+1)2+y2=16及点A(1,0),Q为圆C上一点,AQ的垂直平分线交CQ于M则点M的轨迹方程为 .
查看答案和解析>>
科目:高中数学 来源:2010年浙江省高二上学期期中考试理科数学卷 题型:解答题
(本题满分14分)已知圆C:(x-1)2+(y-2)2=2,过点P(-1,6)作圆C的切线,切点是A,B.(1)求直线PA,PB的方程; (2)求过P点的圆的切线长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com