
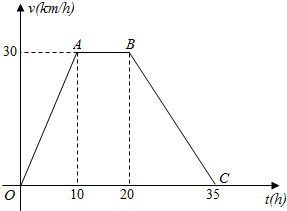
 据气象中心观察和预测:发生于 地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t的函数图象如图所示,过线段OC 上一点T(t,0)作横轴的垂线l,梯形OABC在直线l 左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
据气象中心观察和预测:发生于 地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t的函数图象如图所示,过线段OC 上一点T(t,0)作横轴的垂线l,梯形OABC在直线l 左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).分析 (1)由图象可知:直线OA的方程是:v=3t,直线BC的方程是:v=-2t+70;分段求函数解析式;
(2)求函数在每一段上的函数的取值,从而确定路程s 关于时间t 的函数解析式.
解答 解:(1)当0≤t≤10时,设v=kt,因为函数过点(10,30)((2分)
所以k=3 此时v=3t
当10<t<20时,设v=a,因为函数也过点 (10,30)(2分)
所以v=30
当20≤t≤35时 设v=kt+b,因为函数点(20,30),(30,0),
所以:$\left\{\begin{array}{l}20k+b=30\\ 35k+b=0\end{array}\right.$,解得$\left\{\begin{array}{l}k=-2\\ b=70\end{array}\right.$
综上:v=$\left\{\begin{array}{l}\frac{3}{2}t,t∈[0,10]\\ 30,t∈(10,20)\\-2t+70,t∈[20,35]\end{array}\right.$
(2)由图象可知:
直线OA的方程是:v=3t,直线BC的方程是:v=-2t+70;
当t=4时,v=12,
所以s=$\frac{1}{2}$×4×12=24;
当0≤t≤10时,s=$\frac{1}{2}$t•3t=$\frac{3}{2}$t2;
当10<t≤20时,s=30t-150,
当20<t≤35时,s=-t2+70t+550;
综上可知,s随t变化的规律是
s=$\left\{\begin{array}{l}\frac{3}{2}{t}^{2},0≤t≤10\\ 30t-150,10<t≤20\\-{t}^{2}+70t+550,20<t≤35\end{array}\right.$;
点评 本题考查了分段函数在实际问题中的应用,考查分析问题解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{4}$ | C. | -$\frac{1}{8}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 焦点在x轴上的椭圆 | B. | 焦点在y轴上的椭圆 | ||
| C. | 焦点在x轴上的双曲线 | D. | 焦点在y轴上的双曲线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
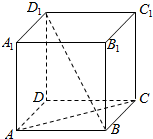 如图,在棱长为2的正方体ABCD-A1B1C1D1中,过AC且与直线D1B平行的截面交D1D于点M,则△MAC的面积为=$\sqrt{6}$.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,过AC且与直线D1B平行的截面交D1D于点M,则△MAC的面积为=$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com