
附加题:(本小题10分,实验班同学必做,其他班学生选做)
是否存在常数a,使得函数f (x)=sin2x+acosx+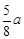 -
-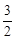 在闭区间
在闭区间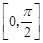 上的最大值为1?若存在,求出对应的a值;若不存在,说明理由.
上的最大值为1?若存在,求出对应的a值;若不存在,说明理由.
存在a=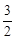 使得f (x)在闭区间
使得f (x)在闭区间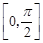 上的最大值为1
上的最大值为1
【解析】解:f (x)=sin2x+acosx+ -
-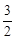
=1-cos2x+acosx+ -
-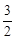 =-cos2x+acosx+
=-cos2x+acosx+ -
-
=-(cosx- a)2+
a)2+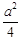 +
+ -
-
∵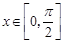 ,∴0≤cosx≤1,
………………1分
,∴0≤cosx≤1,
………………1分
①
若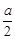 >1,即a>2,则当cosx=1时,f (x)取得最大值,
>1,即a>2,则当cosx=1时,f (x)取得最大值,
f (x)最大值=-(1- a)2+
a)2+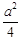 +
+ -
- =
=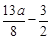 ……………3分
……………3分
令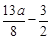 =1,解得
=1,解得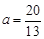 <2(舍去)
……………4分
<2(舍去)
……………4分
②若0≤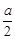 ≤1,即0≤a≤2,则当cosx=
≤1,即0≤a≤2,则当cosx=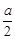 时,f (x)取得最大值,
时,f (x)取得最大值,
f (x)最大值=-( a-
a- a)2+
a)2+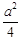 +
+ -
- =
=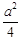 +
+ -
- ……………6分
……………6分
令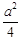 +
+ -
- =1,解得
=1,解得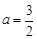 或
或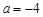 <0(舍去)
……………7分
<0(舍去)
……………7分
③若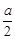 <0,即a<0,则当cosx=0时,f (x)取得最大值,
<0,即a<0,则当cosx=0时,f (x)取得最大值,
f (x)最大值=-(0- a)2+
a)2+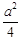 +
+ -
- =
= -
- ……………8分
……………8分
令 -
- =1,解得
=1,解得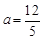 >0(舍去)
……………9分
>0(舍去)
……………9分
综上,存在a=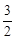 使得f (x)在闭区间
使得f (x)在闭区间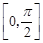 上的最大值为1
……………10分
上的最大值为1
……………10分


科目:高中数学 来源:2011-2012学年安徽省高三摸底考试理科数学 题型:解答题
附加题(本大题共两个小题,每个小题10分,满分 20分,省级示范性高中要
把该题成绩计入总分,普通高中学生选作)
已知 ,
,
(1)判断函数在区间(-∞,0)上的单调性,并用定义证明;
(2)画出该函数在定义域上的图像.(图像体现出函数性质即可)
查看答案和解析>>
科目:高中数学 来源:2010年甘肃省高二第二阶段考试数学理卷 题型:解答题
(本小题满分12分)已知椭圆C: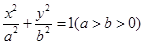 的离心率
的离心率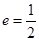 ,且原点
,且原点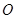 到直线
到直线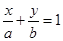 的距离为
的距离为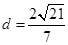 .
.
(Ⅰ)求椭圆的方程 ;
(Ⅱ)过点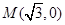 作直线与椭圆C交于
作直线与椭圆C交于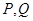 两点,求
两点,求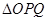 面积的最大值.
面积的最大值.
四.附加题 (共20分,每小题10分)
查看答案和解析>>
科目:高中数学 来源: 题型:
(Ⅰ)设{an}是集合![]() 中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,……
中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,……
将数列{an}各项按照上小下大,左小右大的原则写成如下的三角形数表:
(i)写出这个三角形数表的第四行、第五行各数;
(ii)求a100.
(Ⅱ)(本小题为附加题,如果解答正确,加4分,但全卷总分不超过150分)
设{bn}是集合![]() 中所有的数从小到大排列成的数列,已知bk =1160,求k.
中所有的数从小到大排列成的数列,已知bk =1160,求k.
查看答案和解析>>
科目:高中数学 来源: 题型:
将数列{an}各项按照上小下大,左小右大的原则写成如下的三角形数表:
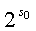
(ⅰ)写出这个三角形数表的第四行、第五行各数;
(ⅱ)求a100.
(Ⅱ)(本小题为附加题)
设{bn}是集合{2t+2s+2r|0≤r<s<t,且r,s,t![]() Z}中所有的数从小到大排列成的数列.
Z}中所有的数从小到大排列成的数列.
已知bk=1160,求k.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com