
(本题14分)某校高二年级研究性学习小组,为了分析2011年我国宏观经济形势,上网查阅了2010年和2011年2-6月我国CPI同比(即当年某月与前一年同月相比)的增长数据(见下表),但2011年4,5,6三个月的数据(分别记为x,y,z)没有查到.有的同学清楚记得2011年2,3,4,5,6五个月的CPI数据成等差数列.
(1)求x,y,z的值;
(2)求2011年2-6月我国CPI的数据的方差;
(3)一般认为,某月CPI达到或超过3个百分点就已经通货膨胀,而达到或超过5个百分点则严重通货膨胀.现随机地从上表2010年的五个月和2011年的五个月的数据中各抽取一个数据,求相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率.
附表:我国2010年和2011年2~6月的CPI数据(单位:百分点.注:1个百分点=1%)
|
年份 |
二月 |
三月 |
四月 |
五月 |
六月 |
|
2010 |
2.7 |
2.4 |
2.8 |
3.1 |
2.9 |
|
2011 |
4.9 |
5.0 |
x |
y |
z |
(1)x=5.1,y=5.2,z=5.3;(2)其平均数为5.1,其方差为0.01;
(3)相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率为0.16.
【解析】本题考查古典概型的计算,涉及等差数列的性质、平均数、方差的计算与列举法的应用,是基础题;注意在列举时做到不重不漏,同时要正确计算
(1)根据题意,结合等差数列的性质,可得该数列的公差为0.1,进而可得x、y、z的值;
(2)由(1)的结论可得2011年中2-6月全部数据,先计算出5个数据的平均数,进而由方差公式计算可得答案;
(3)根据题意,用m表示2010年的数据,n表示2011年的数据,则(m,n)表示随机地从2010年的五个月和2011年的五个月的数据中各抽取一个数据的基本事件,由列举法可得抽取数据的情况,分析可得事件“相同月份2010年通货膨胀,并且2011年严重通货膨胀”包含的基本事件的数目,由古典概型公式,计算可得答案.
解:
(1)依题意得4.9,5.0,x,y,z成等差数列,所以公差d=5.0-4.9=0.1,
故x=5.0+0.1=5.1,y=x+0.1=5.2,z=y+0.1=5.3;
(2)由(1)知2011年2~6月我国CPI的数据为:4.9,5.0,5.1,5.2,5.3
其平均数为:x=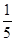 (4.9+5.0+5.1+5.2+5.3)=5.1,其方差为:s2=
(4.9+5.0+5.1+5.2+5.3)=5.1,其方差为:s2=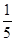 [(4.9-5.1)2+(5.0-5.1)2+(5.1-5.1)2+(5.2-5.1)2+(5.3-5.1)2]=0.01;
[(4.9-5.1)2+(5.0-5.1)2+(5.1-5.1)2+(5.2-5.1)2+(5.3-5.1)2]=0.01;
(3)根据题意,用m表示2010年的数据,n表示2011年的数据,则(m,n)表示随机地从2010年的五个月和2011年的五个月的数据中各抽取一个数据的基本事件,
则所有基本事件有:
(2.7,4.9),(2.7,5.0),(2.7,5.1),(2.7,5.2),(2.7,5.3),
(2.4,4.9),(2.4,5.0),(2.4,5.1),(2.4,5.2),(2.4,5.3),
(2.8,4.9),(2.8,5.0),(2.8,5.1),(2.8,5.2),(2.8,5.3),
(3.1,4.9),(3.1,5.0),(3.1,5.1),(3.1,5.2),(3.1,5.3),
(2.9,4.9),(2.9,5.0),(2.9,5.1),(2.9,5.2),(2.9,5.3);共25个基本事件;
其中满足相同月份2010年通货膨胀,并且2011年严重通货膨胀的基本事件有:(3.1,5.0),(3.1,5.1),(3.1,5.2),(3.1,5.3),有4个基本事件;
所以P=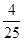 =0.16,即相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率为0.16.
=0.16,即相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率为0.16.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2010年广东省高三第一次月考文科数学卷 题型:解答题
(本题满分14分)
某校高三的某次数学测试中,对其中100名学生的成绩进行分析,按成绩分组,得到的频率分布表如下:
|
组号 |
分组 |
频数 |
频率 |
|
第1组 |
|
15 |
① |
|
第2组 |
|
② |
0.35 |
|
第3组 |
|
20 |
0.20 |
|
第4组 |
|
20 |
0.20 |
|
第5组 |
|
10 |
0.10 |
|
合计 |
|
100 |
1.00 |
(1)求出频率分布表中①、②位置相应的数据;
(2)为了选拔出最优秀的学生参加即将举行的数学竞赛,学校决定在成绩较高的第3、4、5组中分层抽样取5名学生,则第4、5组每组各抽取多少名学生?
(3)为了了解学生的学习情况,学校又在这5名学生当中随机抽取2名进行访谈,求第4组中至少有一名学生被抽到的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com