点P（2，4）在直线ax+y+b=0上的射影是Q（4，3），则a+b的值为 ．
【答案】
分析：由题意可得PQ与直线垂直，直线ax+y+b=0的斜率为2，求出a，进而求出b的值，即可求解a+b．
解答：解：∵P（2，4），Q（4，3），
∴k
PQ=
=-
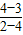
又由P在直线l上的射影为Q
∴直线ax+y+b=0与直线PQ垂直，
∴所求直线ax+y+b=0的斜率为2，所以a=-2，
Q（4，3）在直线-2x+y+b=0上，
代入得：-2×4+3+b=0，解得b=5，
所以a+b=3
故答案为：3．
点评：本题主要考查直线相互垂直的充要条件，以及直线的一般式方程，点与直线的位置关系．
