


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
A.e1·e2=1 B.e1·e2=-1 C.e1·e2=±1 D.|e1·e2|<1
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x) = ax3 + bx2 +cx + d的图像如图所示,则下列判断正确的是
A.a < 0, b < 0, c < 0 B.a > 0, b > 0, c < 0
C.a > 0, b < 0, c > 0 D.a > 0, b > 0, c > 0

查看答案和解析>>
科目:高中数学 来源: 题型:
.函数y=x5-x3-2x,则下列判断正确的是
A.在区间(-1,1)内函数为增函数
B.在区间(-∞,-1)内函数为减函数
C.在区间(-∞,1)内函数为减函数
D.在区间(1,+∞)内函数为增函数
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修1集合练习卷(解析版) 题型:选择题
已知 为非零实数,代数式
为非零实数,代数式 的值所组成的集合为M,则下列
的值所组成的集合为M,则下列
判断正确的是 ( )
A.  B.
B.
 C.
C.
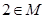 D.
D.

查看答案和解析>>
科目:高中数学 来源:山东省潍坊市09-10学年高二下学期质量调研抽测数学试题 题型:选择题
已知命题 ,
, ;命题
;命题 ,
, ,则下列判断
,则下列判断
正确的是
A.  是真命题 B.
是真命题 B.  是假命题 C.
是假命题 C.  是假命题
D.
是假命题
D.  是假命题
是假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com