
(2007
福建,22)已知函数 .
.
(1)
若k=e,试确定函数f(x)的单调区间;(2)
若k>0,且对于任意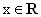 ,f(|x|)>0恒成立,试确定实数k的取值范围;
,f(|x|)>0恒成立,试确定实数k的取值范围;
(3)
设函数F(x)=f(x)+f(-x),求证: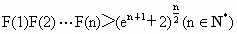 .
. |
解析: (1)由k=e得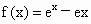 ,所以 ,所以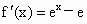 . .
由 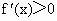 得x>1,故f(x)的单调递增区间是(1,+∞), 得x>1,故f(x)的单调递增区间是(1,+∞),
由 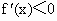 得x<1,故f(x)的单调递减区间是(-∞,1). 得x<1,故f(x)的单调递减区间是(-∞,1).
(2) 由f(|-x|)=f(|x|)可知f(|x|)是偶函数,于是f(|x|)>0对任意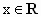 成立等价于f(x)>0对任意x≥0成立. 成立等价于f(x)>0对任意x≥0成立.
由  得x=ln k. 得x=ln k.
①当 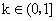 时, 时, ,此时f(x)在[0,+∞)上单调递增,故f(x)≥f(0)=1>0,符合题意. ,此时f(x)在[0,+∞)上单调递增,故f(x)≥f(0)=1>0,符合题意.
②当 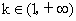 时,ln k>0,当x变化时, 时,ln k>0,当x变化时, 的变化情况如下表: 的变化情况如下表:
由此可得,在 [0,+∞)上f(x)≥f(ln k)=k-kln k.依题意, k-kln k>0,又k>1,∴1<k<e.综合①、②得,实数 k的取值范围是0<k<e.(3 )∵ , ,
∴  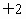 , ,
∴
……
由此得, 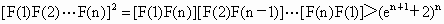 . .
故 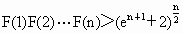 , ,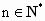 . . |


 应用题作业本系列答案
应用题作业本系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com