
(1)已知数列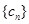 ,其中
,其中 ,且数列
,且数列 为等比数列,求常数p;
为等比数列,求常数p;
(2)设 、
、 是公比不相等的两个等比数列,
是公比不相等的两个等比数列, ,证明:数列
,证明:数列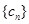 不是等比数列.
不是等比数列.
(1)p=2或p=3. (2)证明略
【解析】本试题主要是考查了等比数列的概念的运用。
(1)第一问中,利用给定的等比数列,结合定义得到p的值
(2)根据设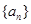 、
、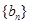 是公比不相等的两个等比数列,
是公比不相等的两个等比数列,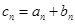 ,那么可验证前几项是否是等比数列来判定结论
,那么可验证前几项是否是等比数列来判定结论
(1)解:因为{cn+1-pcn}是等比数列,
故有:(cn+1-pcn)2=(cn+2-pcn+1)(cn-pcn-1),将cn=2n+3n代入上式,得:
[2n+1+3n+1-p(2n+3n)]2=[2n+2+3n+2-p(2n+1+3n+1)]·[2n+3n-p(2n-1+3n-1)],
即[(2-p)2n+(3-p)3n]2
=[(2-p)2n+1+(3-p)3n+1][(2-p)2n-1+(3-p)3n-1],
整理得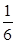 (2-p)(3-p)·2n·3n=0,解得p=2或p=3.
(2-p)(3-p)·2n·3n=0,解得p=2或p=3.
(2)证明:设{an}、{bn}的公比分别为p、q,p≠q,cn=an+bn.
为证{cn}不是等比数列只需证c22≠c1·c3.
事实上,c22=(a1p+b1q)2=a12p2+b12q2+2a1b1pq,
c1·c3=(a1+b1)(a1p2+b1q2)=a12p2+b12q2+a1b1(p2+q2),
由于p≠q,p2+q2>2pq,又a1、b1不为零,因此c22≠c1·c3,故{cn}不是等比数列.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:
已知数列![]() ,其中
,其中![]() 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;![]() 是公差为
是公差为![]() 的等差数列;
的等差数列;![]() 是公差为
是公差为![]() 的等差数列(
的等差数列(![]() ).
).
(1)若![]() ,求
,求![]() ;
;
(2)试写出![]() 关于
关于![]() 的关系式,并求
的关系式,并求![]() 的取值范围;
的取值范围;
(3)续写已知数列,使得![]() 是公差为
是公差为![]() 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省广州东莞五校高三第二次联考理科数学卷 题型:解答题
(本小题满分14分)
已知数列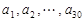 ,其中
,其中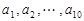 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;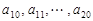 是公差为
是公差为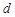 的等差数列;
的等差数列;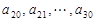 是公差为
是公差为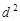 的等差数列(
的等差数列(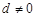 ).
).
(1)若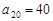 ,求
,求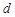 ;
;
(2)试写出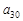 关于
关于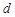 的关系式,并求
的关系式,并求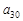 的取值范围;
的取值范围;
(3)续写已知数列,使得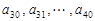 是公差为
是公差为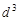 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com