
为了了解某市工厂开展群众体育活动的情况,拟采用分层抽样的方法从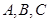 三个区中抽取6个工厂进行调查.已知
三个区中抽取6个工厂进行调查.已知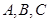 区中分别有27,18,9个工厂.
区中分别有27,18,9个工厂.
(Ⅰ)求从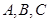 区中应分别抽取的工厂个数;
区中应分别抽取的工厂个数;
(Ⅱ)若从抽得的6个工厂中随机地抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自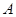 区的概率.
区的概率.
(Ⅰ)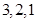 ;(Ⅱ)
;(Ⅱ)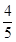
【解析】
试题分析:(Ⅰ)由分层抽样的含义即可得总共有54个工厂,所以抽取的6个工厂占总数的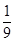 ,所以每个区域的工厂的个数即可求出.
,所以每个区域的工厂的个数即可求出.
(Ⅱ)因为6个被抽到的工厂中,A区有3个工厂,B区有2个,C区有1个.从中抽取两个工厂共有15种情况,一一列举出来.通过数2个工厂中都没来自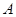 区的共有3种情况,所以符合2个工厂中至少有1个来自
区的共有3种情况,所以符合2个工厂中至少有1个来自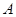 区的共有12种,即可求得结论.
区的共有12种,即可求得结论.
试题解析:解:(Ⅰ)由题可知,每个个体被抽取到得概率为 ;
;
设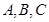 三个区被抽到的工厂个数为
三个区被抽到的工厂个数为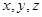 ,则
,则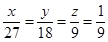
所以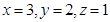 ,故
,故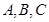 三个区被抽到的工厂个数分别为
三个区被抽到的工厂个数分别为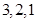
(Ⅱ)设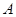 区抽到的工厂为
区抽到的工厂为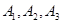 ,
,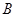 区抽到的工厂为
区抽到的工厂为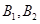 ,
,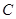 区抽到的工厂为
区抽到的工厂为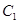
则从6间工厂抽取2个工厂,基本事件有: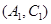 ,
,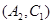 ,
,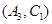 ,
,
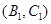 ,
,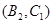 ,
,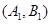 ,
,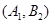 ,
,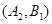 ,
,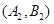 ,
,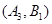 ,
,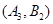
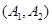 ,
,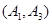 ,
, ,
,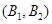 共15种情况;
共15种情况;
2个都没来自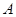 区的基本事件有
区的基本事件有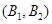 ,
,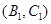 ,
,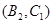 共3种情况
共3种情况
设事件“至少一个工厂来自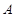 区”为事件
区”为事件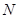 ,则事件
,则事件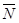 为“2个都没来自
为“2个都没来自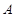 区”
区”
所以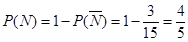
所以,至少有一个工厂来自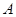 区的概率为
区的概率为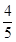
考点:1.分层抽样的思想.2.概率的计算中含至少通常考虑从对立面出发.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三下学期开学考试文科数学 题型:解答题
为了了解某市工厂开展群众体育活动的情况,拟采用分层抽样的方法从A、B、C三个区中抽取6个工厂进行调查.已知A、B、C区中分别有18,27,9个工厂.
(1)求从A、B、C区中应分别抽取的工厂个数;
(2)若从抽得的6个工厂中随机地抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自A区的概率。
查看答案和解析>>
科目:高中数学 来源:2013届江西省高二下学期第二次月考文科数学试卷 题型:解答题
为了了解某市工厂开展群众体育活动的情况,拟采用分层抽样的方法从A、B、C三个区中抽取6个工厂进行调查.已知A、B、C区中分别有18, 27,9个工厂.
(1)求从A、B、C区中应分别抽取的工厂个数;
(2)若从抽得的6个工厂中随机地抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自A区的概率。
查看答案和解析>>
科目:高中数学 来源:广州省2009-2010学年高一学科竞赛 题型:解答题
为了了解某市工厂开展群众体育活动的情况,拟采用分层抽样的方法从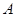 、
、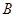 、
、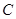 三个区中抽取7个工厂进行调查,已知
三个区中抽取7个工厂进行调查,已知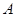 、
、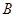 、
、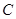 区中分别有18、27、18个工厂。
区中分别有18、27、18个工厂。
(1)求从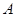 、
、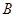 、
、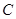 区中应分别抽取的工厂个数;
区中应分别抽取的工厂个数;
(2)若从抽得的7个工厂中随机抽取2个进行调查结果的对比,用列举法计算这2个工厂中至少有1个来自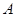 区的概率。
区的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com