
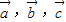 满足
满足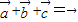 ,且
,且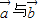 的夹角为135°,
的夹角为135°,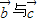 的夹角为120°,
的夹角为120°,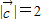 ,则
,则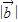 = .
= . 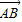 =
=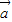 ,
,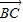 =
=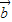 ,
,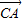 =
=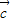 ,则由题意可得B=45°,C=60°,A=75°,且AC=2,|
,则由题意可得B=45°,C=60°,A=75°,且AC=2,|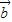 |=BC.利用两角和的正弦公式求得sinA=sin75°
|=BC.利用两角和的正弦公式求得sinA=sin75°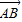 =
=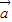 ,
,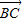 =
=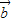 ,
,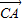 =
=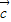 ,显然满足足
,显然满足足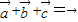 .
.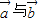 的夹角为135°,
的夹角为135°,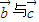 的夹角为120°,
的夹角为120°,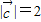 ,可得B=45°,C=60°,∴A=75°,且AC=2,|
,可得B=45°,C=60°,∴A=75°,且AC=2,|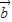 |=BC.
|=BC.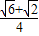 .
.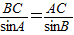 ,即
,即 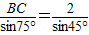 ,解得BC=1+
,解得BC=1+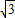 ,
,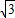 .
.

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源:重难点手册 高中数学·必修4(配人教A版新课标) 人教A版新课标 题型:044
已知向量a,b满足关系式![]() |a-λb|=|λa+b|(λ>0),且a=(cosα,sinα),b=(-
|a-λb|=|λa+b|(λ>0),且a=(cosα,sinα),b=(-![]() ,
,![]() ).
).
(1)试用λ表示向量a与b的数量积;
(2)求a与b所夹锐角的最大值,并求此时λ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com