
如图△ABD≌△CBD,△ABD为等腰三角形.∠BAD=∠BCD=90°,且面ABD⊥面BCD,则下列4个结论中,正确结论的是
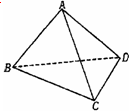
①AC⊥BD;
②△ACD是等腰三角形;
③AB与平面BCD成60°角;
④AB与CD成60°角
①②③
①②④
①③④
②③④
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•商丘三模)如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点.
(2012•商丘三模)如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•江苏一模)(选修4-1 几何证明选讲)
(2013•江苏一模)(选修4-1 几何证明选讲)查看答案和解析>>
科目:高中数学 来源: 题型:
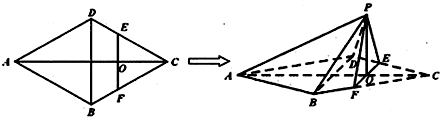
| V1 |
| V2 |
| 4 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
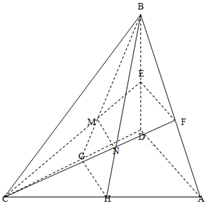 如图,在四面体A-BCD中,有CB=CD,平面ABD⊥平面BCD,点E、F分别为BD,AB的中点,MN∥平面ABD.
如图,在四面体A-BCD中,有CB=CD,平面ABD⊥平面BCD,点E、F分别为BD,AB的中点,MN∥平面ABD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com