
分析:α是三角形的内角,若
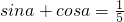
?1+2sina•cosa=

?a是钝角,1-2sina•cosa=

?sina-cosa=

,从而可求sina,cosa,tana可求.
解答:∵α是三角形的内角,若
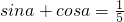
,①
∴(sina+cosa)
2=

,即1+2sina•cosa=

,
∴2sina•cosa=-

<0,
∴a为钝角;
∴sina>0,cosa<0;
∴(sina-cosa)
2=1-2sina•cosa=

,
∴sina-cosa=

,②
由①②解得sina=

,cosa=
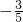
;
∴tana=

.
故答案为:

.
点评:本题考查同角三角函数间的基本关系,关键在于判断a为钝角,着重考查解方程的能力,属于中档题.

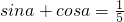 ,则tana=________.
,则tana=________.