解:(1)证明:由{an}为等差数列可得an-an-1=d(n≥2),则1/a{1}-1/a{2}=a{2}-a{1}/a{1a{2}}=d/a{1a{2}}得证;{C/{0{2}}}{a{1}}-{C/{1{2}}}{a{2}}+{C/{2{2}}}{a{3}}=1/a{1}-2/a{2}+1/a{3}=1/a{1}-1/a{2}+1/a{3}-1/a{2}=a{2}-a{1}/a{1a{2}}+a{2}-a{3}/a{2a{3}}=d•a{3}-a{1}/a{1a{2}a{3}}=2d2/a{1a{2}a{3} }得证;{C/{0{3}}}{a{1}}-{C/{1{3}}}{a{2}}+{C/{2{3}}}{a{3}}-{C/{3{3}}}{a{4}}=1/a{1}-3/a{2}+3/a{3}-1/a{4}=(1/a{1}-1/a{4})-(3/a{2}-3/a{3})=3d/a{1a{4}}-3d/a{2a{3}}=3d•a{2}a{3}-a{1}a{4} /a{1a{2}a{3}a{4}}=3d•2 d /a{1a{2}a{3}a{4}}=6d3/a{1a{2}a{3}a{4}}得证.(2)结论:{C/{0{n-1}}}{a{1}}-{C/{1{n-1}}}{a{2}}+{C/{2{n-1}}}{a{3}}-…+(-1){n+1/C{{n-1}{n-1}}}{a{n}}=(n-1)!d{n-1}/a{1a{2}…a{n}},证:①当n=2,3,4时,等式成立,②假设当n=k时,{C/{0{k-1}}}{a{1}}-{C/{1{k-1}}}{a{2}}+{C/{2{k-1}}}{a{3}}-+(-1){k+1/C{{k-1}{k-1}}}{a{k}}=(k-1)!d{k-1}/a{1a{2}a{k}}成立,那么当n=k+1时,因为Cki-1=Ck-1i-1+Ck-1k-2,所以{C/{0{k}}}{a{1}}-{C/{1{k}}}{a{2}}+{C/{2{k}}}{a{3}}-+(-1){k+2/C{{k}{k}}}{a{k+1}}={C/{0{k-1}}}{a{1}}-{C/{1{k-1}}+{C}{0{k-1}}}{a{2}}+{C/{2{k-1}}+{C}{1{k-1}}}{a{3}}-+(-1){k+1}({C/{k-1{k-1}}+{C}{{k-2}{k-1}})}{a{k}}+(-1){k+2/C{{k-1}{k-1}}}{a{k+1}}=({C/{0{k-1}}}{a{1}}-{C/{1{k-1}}}{a{2}}+{C/{2{k-1}}}{a{3}}-+(-1){k+1/C{{k-1}{k-1}}}{a{k}})-({C/{0{k-1}}}{a{2}}-{C/{1{k-1}}}{a{3}}+{C/{2{k-1}}}{a{4}}-+(-1){k+1/C{{k-1}{k-1}}}{a{k+1}})=(k-1)!d{k-1}/a{1a{2}a{k}}-(k-1)!d{k-1}/a{2a{3}a{k}}=(k-1)!d{k-1}/a{1a{2}a{k}}(a{k+1}-a{1})=k!d{k}/a{1a{2}a{k}a{k+1}},所以,当n=k+1时,结论也成立.综合①②知,{C/{0{n-1}}}{a{1}}-{C/{1{n-1}}}{a{2}}+{C/{2{n-1}}}{a{3}}-+(-1){n+1/C{{n-1}{n-1}}}{a{n}}=(n-1)!d{n-1}/a{1a{2}a{n}}对n≥2都成立.

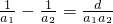 ;
;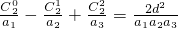 ;
;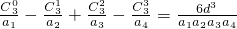 ;
;

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案