Question

已知偶函数f（x）的周期为6，且当0≤x≤3时，f（x）=x²-4x+4，g（x）=f（x）-，则g（x）的零点有

1. A.
   21个
2. B.
   22个
3. C.
   23个
4. D.
   24个

Answer 1

C
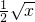分析：先根据函数的周期性和偶函数图象的性质画出y=f（x）的图象，以及y=的图象，结合图象求出在[0，6]上和在[6，12]上的交点个数，再求出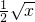=4时的解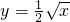，的图象在y=f（x）的图象上方的临界点，再由周期性和图象求出g（x）=f（x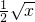）-|的零点个数．
解答：由题意得，当0≤x≤3时，f（x）=x²-4x+4=（x-2）²，
由偶函数f（x）的周期为6画出函数f（x）的图象，并在同一坐标系中画出y=的图象，

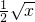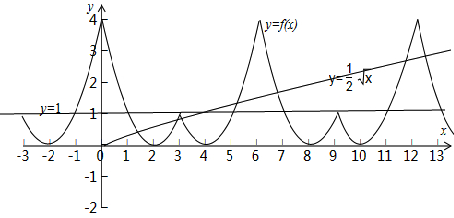
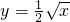由图得，在[0，6]上y=f（x）与的图象有4个交点，在[6，12]上有2个交点，即以后相交的每个周期都有2个交点，
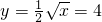再由得，x=64，则区间[0，64]共有10个周期和个周期，而个周期的图象如[6，10]上的图象：只有1个交点，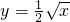
∵在[0，+∞）上递增，
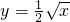∴y=f（x）与有且仅有：4+9×2+1=23个交点，
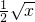则g（x）=f（x）-有23个零点，
故选C．
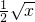点评：本题考查函数的零点个数的求法以及函数性质的应用，关键是根据函数f（x）性质正确作出其图象，再将函数g（x）=f（x）-的零点个数的问题，转化为两个函数交点个数问题，此一转化使得本题的求解变得较容易，注意求出临界点考查了数形结合思想．