Question

如图所示，用一段长为20米的篱笆围成一个一边靠墙的矩形鸡圈ABCD，设AB＝x，矩形ABCD的面积为S．

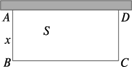
(1)求S关于x的函数解析式，并指明函数的定义域；

(2)求函数S(x)的值域；

(3)试问该函数有最小值吗？为什么？

Answer 1

答案：
解析：

解：∵AB＝x， 　　∴BC＝20－2x． 　　(1)S(x)＝AB·BC＝x(20－2x)＝－2x2＋20x． 　　由于矩形的各边均为正数，则有 　　即0＜x＜10， 　　函数的定义域为(0，10)． 　　(2)∵S(x)＝－2x2＋20x＝－2(x－5)2＋50，而函数的定义域为(0，10)， 　　∴当x＝5时，函数S(x)有最大值为50． 　　∴函数S(x)的值域为(0，50]． 　　(3)函数S(x)没有最小值．当x很小时，由S(x)＝AB·BC＜20x， 　　故在(0，5]内S(x)随x的值减小而减小，即函数S(x)没有最小值． 　　思路分析：矩形的面积等于长与宽的积，由AB＝x，可由x表示BC，即可求得S(x)，在求定义域时要充分考虑到x的实际意义，求值域可利用配方法．