
【题目】如图,半径为1的半圆O与等边三角形ABC夹在两平行线l1 , l2之间,l∥l1 , l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点.设弧 ![]() 的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2 , 则函数y=f(x)的图象大致是( )
的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2 , 则函数y=f(x)的图象大致是( ) 
A.
B.
C.
D.
【答案】D
【解析】解:当x=0时,y=EB+BC+CD=BC= ![]() ;
;
当x=π时,此时y=AB+BC+CA=3× ![]() =2
=2 ![]() ;
;
当x= ![]() 时,∠FOG=
时,∠FOG= ![]() ,三角形OFG为正三角形,此时AM=OH=
,三角形OFG为正三角形,此时AM=OH= ![]() ,
,
在正△AED中,AE=ED=DA=1,
∴y=EB+BC+CD=AB+BC+CA﹣(AE+AD)=3× ![]() ﹣2×1=2
﹣2×1=2 ![]() ﹣2.如图.
﹣2.如图.
又当x= ![]() 时,图中y0=
时,图中y0= ![]() +
+ ![]() (2
(2 ![]() ﹣
﹣ ![]() )=
)= ![]() >2
>2 ![]() ﹣2.
﹣2.
故当x= ![]() 时,对应的点(x,y)在图中红色连线段的下方,对照选项,D正确.
时,对应的点(x,y)在图中红色连线段的下方,对照选项,D正确.
故选D.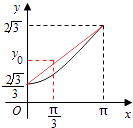
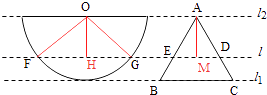
由题意可知:随着l从l1平行移动到l2 , y=EB+BC+CD越来越大,考察几个特殊的情况,计算出相应的函数值y,结合考查选项可得答案.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】定义“正对数”:ln+x= ![]() ,现有四个命题:
,现有四个命题:
①若a>0,b>0,则ln+(ab)=bln+a;
②若a>0,b>0,则ln+(ab)=ln+a+ln+b;
③若a>0,b>0,则 ![]() ;
;
④若a>0,b>0,则ln+(a+b)≤ln+a+ln+b+ln2.
其中的真命题有(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)已知过原点的动直线![]() 与圆
与圆![]()
![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]()
![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=( ) 
A.8
B.9
C.10
D.11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosC+(cosA﹣ ![]() sinA)cosB=0.
sinA)cosB=0.
(1)求角B的大小;
(2)若a+c=1,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小波以游戏方式决定是参加学校合唱团还是参加学校排球队,游戏规则为:以0为起点,再从A1 , A2 , A3 , A4 , A5 , A6 , A7 , A8(如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X.若X=0就参加学校合唱团,否则就参加学校排球队. 
(1)求小波参加学校合唱团的概率;
(2)求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,圆
中,圆![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 分别与圆
分别与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.

(Ⅰ)若![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
(Ⅱ)若直线![]() 过点
过点![]() ,证明:
,证明:![]() 为定值,并求此定值.
为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,若
,若![]() 对一切
对一切![]() 恒成立, 给出以下结论:
恒成立, 给出以下结论:
①![]() ;
;
②![]() ;
;
③![]() 的单调递增区间是
的单调递增区间是![]()
![]() ;
;
④函数![]() 既不是奇函数也不是偶函数;
既不是奇函数也不是偶函数;
⑤存在经过点![]() 的直线与函数
的直线与函数![]() 的图象不相交.其中正确结论的个数为( )
的图象不相交.其中正确结论的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com