

 A1D1.
A1D1. ,然后求四面体EFGB1的体积.
,然后求四面体EFGB1的体积. A1D1,使EH∥平面FGB1 (6分)
A1D1,使EH∥平面FGB1 (6分) ),F(0,1,1),B1(1,2,1),G(
),F(0,1,1),B1(1,2,1),G( ,2,0),
,2,0), ,
, ,
, ,
,
 得
得 ,∴x=-2,y=2,
,∴x=-2,y=2,
 =
=
 ,
, ,
, ,
, =
= ,
, .
. .
. (12分)
(12分)

 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
 (2009•湖北模拟)如图,长方体AC1中,AB=2,BC=AA1=1,E、F、G分别为棱DD1、D1C1、BC的中点,
(2009•湖北模拟)如图,长方体AC1中,AB=2,BC=AA1=1,E、F、G分别为棱DD1、D1C1、BC的中点,查看答案和解析>>
科目:高中数学 来源:2014届江西省高二第四次月考文科数学试卷(解析版) 题型:解答题
如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.
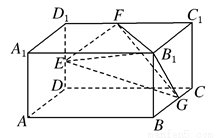
(1)求证:平面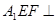 平面
平面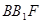 ;
;
(2)在底面A1D1上有一个靠近D1的四等分点H,求证: EH∥平面FGB1;
(3)求四面体EFGB1的体积.
查看答案和解析>>
科目:高中数学 来源:2014届江西省高二第二次月考文科数学试卷(解析版) 题型:解答题
如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.
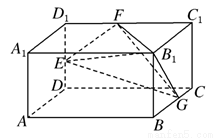
(1)求证:平面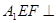 平面
平面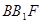 ;
;
(2)在底面A1D1上有一个靠近D1的四等分点H,求证: EH∥平面FGB1;
(3)求四面体EFGB1的体积.
查看答案和解析>>
科目:高中数学 来源:2008-2009学年湖北省百所重点中学高三第二次联考数学试卷(文科)(解析版) 题型:解答题
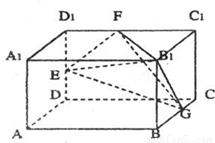
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com