
| A. | [6,9] | B. | [3$\sqrt{3}$+3,9) | C. | (6,9] | D. | (3$\sqrt{3}$+3,9] |
分析 由正弦定理可得:$\frac{b}{sinB}$=$\frac{c}{sinC}$=$\frac{a}{sinA}$=$\frac{3}{sin60°}$=2$\sqrt{3}$,b=2$\sqrt{3}$sinB,c=2$\sqrt{3}$sinC,于是a+b+c=3+2$\sqrt{3}$sinB+2$\sqrt{3}$sin( $\frac{2π}{3}$-B)化简整理即可得出.
解答 解:由正弦定理可得:$\frac{b}{sinB}$=$\frac{c}{sinC}$=$\frac{a}{sinA}$=$\frac{3}{sin60°}$=2$\sqrt{3}$,
∴b=2$\sqrt{3}$sinB,c=2$\sqrt{3}$sinC,
∴a+b+c=3+2$\sqrt{3}$sinB+2$\sqrt{3}$sinC=3+2$\sqrt{3}$sinB+2$\sqrt{3}$sin($\frac{2π}{3}$-B)=3+3$\sqrt{3}$sinB+3cosB=6sin(B+$\frac{π}{6}$)+3,
∵$\frac{π}{6}$<B<$\frac{π}{2}$,
∴$\frac{π}{3}$<B+$\frac{π}{6}$<$\frac{2π}{3}$,
∴sin(B+$\frac{π}{6}$)∈($\frac{\sqrt{3}}{2}$,1],
∴(a+b+c)∈(3+3$\sqrt{3}$,9].
故选:D.
点评 本题主要考查正弦定理、诱导公式、两角和与差的余弦公式等基础知识,考查了考生运算求解的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -$\frac{3}{4}$ | C. | 0 | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
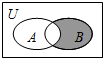 设全集U是实数集R,集合A={y|y=3x,x>0},B={x|y=$\sqrt{2x-{x}^{2}}$},则图中阴影部分所表示的集合是( )
设全集U是实数集R,集合A={y|y=3x,x>0},B={x|y=$\sqrt{2x-{x}^{2}}$},则图中阴影部分所表示的集合是( )| A. | {x|0≤x<1} | B. | {x|0≤x≤1} | C. | {x|1<x<2} | D. | {x|1<x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com