Question

下面有3个命题，①三棱锥的四个面的面积分别为S₁ S₂S₃S₄，则S_l+S₂+S₃＞S₄，②任意四面体均有外接球，③过两异面直线外一点，有且只有一条直线与两异面直线相交，其中，真命题的个数为（ ）
A．0
B．l
C．2
D．3

Answer 1

【答案】分析：①作出一个三棱锥，不妨证明三个侧面的面积大于底面的面积，分顶点在底面的射影在底面三角形内部和外部两种情况证明结论成立；
②从分析四面体的一个面一定有外接圆入手，找出过该外接圆圆心的一条垂线，可知该垂线上必有一点到四面体的四个顶点的距离相等，说明任意四面体均有外接球
③通过作图能够直观的分析得到，如果两条异面直线外的一点，在过两条异面直线中的一条且和另一条平行的平面上，则过该点不会有直线同时和两条异面直线相交．
解答：解：①如图，

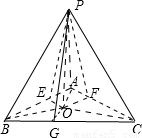
设三棱锥P-ABC三个侧面的面积分别为S_△PAB=S₁，S_△PAC=S₂，S_△PBC=S₃，底面S_△ABC=S₄，
过顶点P作PO⊥面ABC，垂足为O，当O在底面三角形ABC内部时，过O分别作三边垂线OE，OF，OG，连接PE，PF，PG，
则PE⊥AB，PF⊥AC，PG⊥BC，因为PE＞OE，PF＞OF，PG＞OG，则S₁＞S_△ABO，S₂＞S_△ACO，S₃＞S_△BCO，
所以，S_l+S₂+S₃＞S_△ABO+S_△ACO+S_△BCO=S₄
当O在底面三角形ABC外部时，如图，

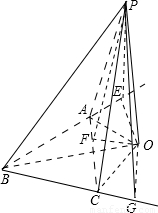
过O分别作三边及其延长线的垂线OE，OF，OG，连接PE，PF，PG，则PE⊥AB，PF⊥AC，PG⊥BC，因为PE＞OE，PF＞OF，
PG＞OG，则S₁＞S_△ABO，S₂＞S_△ACO，S₃＞S_△BCO，而S_△ABO+S_△ACO+S_△BCO＞S_△ABC=S₄
所以，S_l+S₂+S₃＞S_△ABO+S_△ACO+S_△BCO＞S₄
综上，命题①正确．
②四面体的一个面上的三个顶点组成一个三角形，此三角形必有一个外接圆，过此外接圆的圆心且垂直于三角形所在的平面的直线上任意一点到三个顶点的距离相等，在这条直线上总能找到一点，使四面体的第四个点到此点的距离等于此点到其它三点的距离（即球心）．所以，任意四面体均有外接球正确；
③过两异面直线外一点，有且只有一条直线与两异面直线相交，不正确．如：

a和b是两条异面直线，α为过a且与b平行的平面，若两条异面直线外的点O在平面α上，则过O的直线要么只与a相交，要么只与b相交．
所以，过两异面直线外一点，有且只有一条直线与两异面直线相交错误．
所以，正确的命题只有①②．
故选C．
点评：本题是命题的真假判断与应用，考查了学生的空间想象和思维能力，对初学立体图形的学生来说，此题属于难题．