
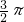 米3的无盖圆锥形容器,容器的底面半径为r(米),而制造底面的材料每平方米30元,制造容器壁的材料每平方米20元,设计时材料厚度忽略不计.
米3的无盖圆锥形容器,容器的底面半径为r(米),而制造底面的材料每平方米30元,制造容器壁的材料每平方米20元,设计时材料厚度忽略不计.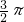 米3,我们易得容器壁的造价为:40πr
米3,我们易得容器壁的造价为:40πr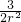
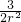
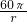 (r>0);
(r>0);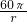 (r>0)=30π(r2+
(r>0)=30π(r2+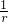 +
+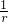 )≥90≈283元,
)≥90≈283元,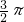 米3,我们设底面半径为r,易求出底面面积,及侧(容器壁)面积,然后再根据制造底面的材料每平方米30元,制造容器壁的材料每平方米20元,我们可得到容器的成本y(元)表示为r的函数的解析式;
米3,我们设底面半径为r,易求出底面面积,及侧(容器壁)面积,然后再根据制造底面的材料每平方米30元,制造容器壁的材料每平方米20元,我们可得到容器的成本y(元)表示为r的函数的解析式;

科目:高中数学 来源: 题型:
| 3 | 2 |
查看答案和解析>>
科目:高中数学 来源:2010年安徽省高考数学最后冲刺试卷(六)(解析版) 题型:解答题
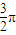 米3的无盖圆锥形容器,容器的底面半径为r(米),而制造底面的材料每平方米30元,制造容器壁的材料每平方米20元,设计时材料厚度忽略不计.
米3的无盖圆锥形容器,容器的底面半径为r(米),而制造底面的材料每平方米30元,制造容器壁的材料每平方米20元,设计时材料厚度忽略不计.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com