
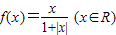 时,则下列结论不正确是 .
时,则下列结论不正确是 .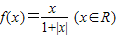 为奇函数,根据函数奇偶性的定义可判断其真假;
为奇函数,根据函数奇偶性的定义可判断其真假;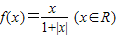 在R上单调递增且值域为(-1,1),则函数y=|f(x)|的值为(0,1),由此可判断(2)的正误;
在R上单调递增且值域为(-1,1),则函数y=|f(x)|的值为(0,1),由此可判断(2)的正误; 为奇函数
为奇函数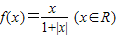 的在R上单调递增,且值域为(-1,1)
的在R上单调递增,且值域为(-1,1)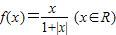 的在R上单调递增,
的在R上单调递增,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012年江苏省无锡市辅仁高级中学高三3月联考数学试卷(解析版) 题型:解答题
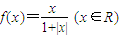 时,则下列结论不正确是 .
时,则下列结论不正确是 .查看答案和解析>>
科目:高中数学 来源:2010年江苏省南通市高考数学信息试卷(一)(解析版) 题型:解答题
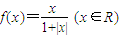 时,则下列结论不正确是 .
时,则下列结论不正确是 .查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市东城区东直门中学高三数学提高测试试卷5(理科)(解析版) 题型:选择题
 时,则下列结论不正确的是( )
时,则下列结论不正确的是( )查看答案和解析>>
科目:高中数学 来源:2011年河南省洛阳市宜阳实验中学高三3月质量调研数学试卷(理科)(解析版) 题型:选择题
 时,则下列结论不正确的是( )
时,则下列结论不正确的是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com