
| 1 |
| 2 |
| �� |
| 32 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| �� |
| 32 |
| 23 |
| 12 |
| ��x |
| 32 |
| 3�� |
| 4 |
| ��x |
| 32 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 3 |
| 5 |
| 12 |
| 1 |
| 2 |
| 1 |
| 3 |
|
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 6 |
| 1 |
| 2 |
| 7 |
| 6 |
| 1 |
| 3 |
| 7 |
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 6 |
| 7 |
| 12 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
|
| 23 |
| 12 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x |
| x2+1 |
| 1 |
| 3 |
| 3 |
| 4 |
| x |
| x2+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij�л����о�����������ÿ�컷����Ⱦ������е����о�����һ�����ۺ���Ⱦָ��![]() ��ʱ��x(Сʱ)�Ĺ�ϵΪ
��ʱ��x(Сʱ)�Ĺ�ϵΪ![]() ����
����![]() ����2a��
����2a��![]() ������aΪ�������йصIJ�������
������aΪ�������йصIJ�������![]() ������ÿ����
������ÿ����![]() �����ֵ��Ϊ������ۺ���Ⱦָ����������M(a) ��
�����ֵ��Ϊ������ۺ���Ⱦָ����������M(a) ��
(��)��t��![]() ��
��![]() ����t��ȡֵ��Χ��
����t��ȡֵ��Χ��
(��) ����M(a)�Ľ���ʽ��
(��) Ϊ��ǿ�Ի�����Ⱦ�����Σ��������涨ÿ����ۺ���Ⱦָ�����ó���2������Ŀǰ�����ĵ��ۺ���Ⱦָ���Ƿꣿ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�꽭�ո߿���ѧԤ���Ծ��������棩 ���ͣ������
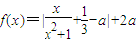 ��x��[{0��24}]������a�������йصIJ�������
��x��[{0��24}]������a�������йصIJ�������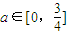 ������ÿ��f��x�������ֵΪ������ۺ���Ⱦָ����������M��a����
������ÿ��f��x�������ֵΪ������ۺ���Ⱦָ����������M��a����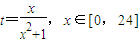 ����t��ȡֵ��Χ��
����t��ȡֵ��Χ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010�꽭��ʡ��ͨ�к����ظ߿��ع�α�ר������ѧ�Ծ���һ���������棩 ���ͣ������
 ��x��[{0��24}]������a�������йصIJ�������
��x��[{0��24}]������a�������йصIJ������� ������ÿ��f��x�������ֵΪ������ۺ���Ⱦָ����������M��a����
������ÿ��f��x�������ֵΪ������ۺ���Ⱦָ����������M��a���� ����t��ȡֵ��Χ��
����t��ȡֵ��Χ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com